Question 995635: I have to use one of the arithmetic series formula. The arithmetic series 5 + 9 + 13 +...+ tn has a sum of 945. How many terms does this series have?
Found 2 solutions by MathLover1, atique.ah:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 , ,  , ,  ,+...+ ,+...+ 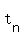 has a sum of has a sum of 
I can see from the sequence  , ,  , ,  , ... that each term is , ... that each term is  more than the previous term. more than the previous term.
The first term is  . .
The second term is  . .
The third term is  fours plus fours plus  : :  . .
Thus the nth term must be 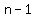 fours plus fours plus  . .
That is  . .
Thus the  term series is: term series is:
 + ... + + ... +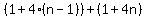
You can find the sum of this series by writing it forward and backwards and then adding down
 + ... + ... 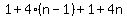
 + ... + 9 + 5}}} + ... + 9 + 5}}}
 + ... + + ... + 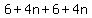
Since there are  terms in the series, we have terms in the series, we have

and thus

since given the sum
 solve for solve for  to find how many terms are in this sequence to find how many terms are in this sequence



 ....disregard negative solution ....disregard negative solution

so, there is  terms in your sequence, and they are terms in your sequence, and they are
 , ,  , ,  , , , ,  , ,  , , , ,  , ,  , , , ,  , , 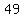 , , , , 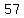 , , 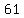 , ,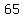 , , 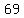 , ,  , , , , 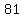 , , 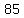
check their sum:


Answer by atique.ah(27)   (Show Source): (Show Source):
|
|
|