SOLUTION: a garrison of 600 men had provision for 25 days.after 9 days an addition of men was made and the remaining provision latest only for 4 days.find the number added.

Algebra ->  Test -> SOLUTION: a garrison of 600 men had provision for 25 days.after 9 days an addition of men was made and the remaining provision latest only for 4 days.find the number added.      Log On


   

Question 995562: a garrison of 600 men had provision for 25 days.after 9 days an addition of men was made and the remaining provision latest only for 4 days.find the number added.
Found 2 solutions by josmiceli, MathTherapy:
Answer by josmiceli(19441) About Me  (Show Source):
You can put this solution on YOUR website!
In 1 day, the 600 men consume +1%2F25+
of the provisions
----------------
In 1 day, each of the 600 men consume
+%28+1%2F600+%29%2A%28+1%2F25+%29+=+1%2F15000+ of the
provisions
----------------
After 9 days, the 600 men consume +9%2F25+
of the provisions
That means there is +1+-+9%2F25+=+16%2F25+
of the provisions left
-----------------
+16%2F25+ was consumed in 4 days
[ rate for 1 man in 1 day ] x [ 600 + n men] x [ 4 days ] = [ fraction of provisions left ]
+%28+1%2F15000+%29%2A4%2A%28+600+%2B+n+%29+=+16%2F25+
+4%2A%28+600+%2B+n+%29+=+%28+16%2F25+%29%2A15000+
+600+%2B+n+=+%28+4%2F25+%29%2A15000+
+n+=+2400+-+600+
+n+=+1800+
1800 men were added
-------------------
check:
+1800+%2B+600+=+2400+
+%28+1%2F15000+%29%2A4%2A2400+=+.64+
+16%2F25+=+.64+
OK
Definitely get a 2nd opinion on this.
It is a little tricky for me

Answer by MathTherapy(10551) About Me  (Show Source):
You can put this solution on YOUR website!

a garrison of 600 men had provision for 25 days.after 9 days an addition of men was made and the remaining provision latest only for 4 days.find the number added.
M+=+k%28c%29%2FT, with:
M being number of men

k being constant of variation

c being consumption

T being time
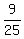600+=+k%281%29%2F25
600+=+k%2F25
k+=+600%2825%29, or 15,000



In 9 days, we get:
M+=+k%28c%29%2FT
600+=+15000%28c%29%2F9
600+=+15000c%2F9
15000c+=+600%289%29
c, or fraction consumed in 9 days = 600%289%29%2F15000, or 9%2F25+


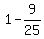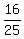In 9 days, 9%2F25 of the provision was consumed by 600 men, so 1+-+9%2F25, or 16%2F25 of provision remain

With additional men being A, we get:
M+%2B+A+=+k%28c%29%2FT
600+%2B+A+=+15000%2816%2F25%29%2F4
600+%2B+A+=+600%2816%29%2F4
600 + A = 2,400

A, or additional men = 2,400 - 600, or highlight_green%281800%29