A group of workers was put on a job. From the second day onwards one
worker was withdrawn each day. The work was finished when the last
worker was withdrawn. If no worker was withdrawn at any stage, the
group would have finished the job in two-thirds time. How many workers
were there in the group?
Let n be the number of workers.
>>...The work was finished when the last worker was withdrawn...<<
Since the nth worker was withdrawn on the nth day, the number of days
required to finish the job was n days.
We will assume that all n workers worked at the same rate. Let the
fraction of a job per day that each worker could do be r. Suppose
they finished in n days.
The 1st worker only worked 1 day before he was withdrawn, so his
fraction of the job was r.
The 2nd worker worked 2 days before he was withdrawn, so his
fraction of the job was 2r.
The 3rd worker worked 3 days before he was withdrawn, so his
fraction of the job was 3r.
...(etc.)...
The nth worker worked n days before he was withdrawn, so his
fraction of the job was nr.
If we add the fractions of the job each did it should add to
one job
r + 2r + 3r + ... + nr = 1
>>...If no worker was withdrawn at any stage, the group would have
finished the job in two-thirds time...<<
If all n workers had stayed on the job throughout, it would
have taken only  n days instead of the n days.
Then each worker would have worked for
n days instead of the n days.
Then each worker would have worked for  n days, and
since the fraction of the job each worker would have
completed per day would have been r, in
n days, and
since the fraction of the job each worker would have
completed per day would have been r, in  n days each
worker would have done this fraction of the job --->
n days each
worker would have done this fraction of the job --->  nr.
Since there were n workers, the sum of all the fractions
of the job they would have done would have been n times the
fraction each worker would have done. So we multiply
nr.
Since there were n workers, the sum of all the fractions
of the job they would have done would have been n times the
fraction each worker would have done. So we multiply  nr
by n and get
nr
by n and get  nēr.
Since the n workers would have completed one full job, we set
that = 1 job:
nēr.
Since the n workers would have completed one full job, we set
that = 1 job:
 nēr = 1
So we have this system of equations:
r + 2r + 3r + ... + nr = 1
nēr = 1
So we have this system of equations:
r + 2r + 3r + ... + nr = 1
 nēr = 1
The left side of the first equation is the sum of an
arithmetic series, so we use the formula
Sn = n(a1+an)/2
where a1 = r and an = nr
r + 2r + 3r + ... + nr = n(r+nr)/2
Since the left side equals 1, so does the right side:
n(r+nr)/2 = 1
Multiply both sides by 2 to clear the fraction
n(r+nr) = 2
nr+nēr = 2
Now we work on the second equation
nēr = 1
The left side of the first equation is the sum of an
arithmetic series, so we use the formula
Sn = n(a1+an)/2
where a1 = r and an = nr
r + 2r + 3r + ... + nr = n(r+nr)/2
Since the left side equals 1, so does the right side:
n(r+nr)/2 = 1
Multiply both sides by 2 to clear the fraction
n(r+nr) = 2
nr+nēr = 2
Now we work on the second equation
 nēr = 1
Multiply both sides by 3 to clear the fraction
2nēr = 3
So now our simplified system of equations is
nr + nēr = 2
2nēr = 3
Solve the second equation for r:
r =
nēr = 1
Multiply both sides by 3 to clear the fraction
2nēr = 3
So now our simplified system of equations is
nr + nēr = 2
2nēr = 3
Solve the second equation for r:
r = 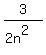 Substitute in the first equation:
nr + nēr = 2
n(
Substitute in the first equation:
nr + nēr = 2
n(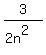 ) + nē
) + nē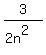 = 2
which simplifies to
= 2
which simplifies to
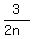 +
+  = 2
Multiply through by LCD = 2n to clear of fractions:
(2n)
= 2
Multiply through by LCD = 2n to clear of fractions:
(2n)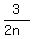 + (2n)
+ (2n) = (2n)2
3 + 3n = 4n
Subtract 3n from both sides
3 = 4n - 3n
3 = n
So there were three workers, and it took
three days to finish the job.
-----------------------------------------
Checking: If all 3 workers had stayed on the job,
the job would have been finished in 2 days instead
of 3, so in one day, all three workers would have
done 1/2 the job and each worker would have done
1/3 of 1/2 of the job, or 1/6 of the job.
So the first day there were 3 workers on the job,
each doing 1/6 of the job. 3 times 1/6 is 1/2, so
half the job got finished on the first day only.
The second day there were 2 workers on the job,
each doing 1/6 of the job, 2 times 1/6 is 1/3, so
1/3 of the job got finished on the second day only.
The third day there was only 1 worker on the job, and
he did 1/6 of the job, so 1/6 of the job got finished
at the end of the second day.
If we add together
1. the 1/2 of the job that got done on the first day,
2. the 1/3 of the job that got done on the second day,
and
3. the 1/6 of the job that got done on the third day,
we get 1/2 + 1/3 + 1/6 = 3/6 + 2/6 + 1/6 = 6/6 = 1 job.
So 3 workers is correct.
Edwin
= (2n)2
3 + 3n = 4n
Subtract 3n from both sides
3 = 4n - 3n
3 = n
So there were three workers, and it took
three days to finish the job.
-----------------------------------------
Checking: If all 3 workers had stayed on the job,
the job would have been finished in 2 days instead
of 3, so in one day, all three workers would have
done 1/2 the job and each worker would have done
1/3 of 1/2 of the job, or 1/6 of the job.
So the first day there were 3 workers on the job,
each doing 1/6 of the job. 3 times 1/6 is 1/2, so
half the job got finished on the first day only.
The second day there were 2 workers on the job,
each doing 1/6 of the job, 2 times 1/6 is 1/3, so
1/3 of the job got finished on the second day only.
The third day there was only 1 worker on the job, and
he did 1/6 of the job, so 1/6 of the job got finished
at the end of the second day.
If we add together
1. the 1/2 of the job that got done on the first day,
2. the 1/3 of the job that got done on the second day,
and
3. the 1/6 of the job that got done on the third day,
we get 1/2 + 1/3 + 1/6 = 3/6 + 2/6 + 1/6 = 6/6 = 1 job.
So 3 workers is correct.
Edwin