Question 995119: I really need help with this problem. Please show every step by step. Thank you
The polynomial of degree 4, P(x) has a root of multiplicity 2 at x=2 and roots of multiplicity 1 at x=0 and x=−2 . It goes through the point (5,252) .
Find a formula for P(x) .
Answer by ikleyn(52864)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The polynomial of degree 4, P(x) has a root of multiplicity 2 at x=2 and roots of multiplicity 1 at x=0 and x=−2. It goes through the point (5,252).
Find a formula for P(x).
----------------------------------------------------------------------
According to the given information about the roots, the polynomial is
P(x) =  = = 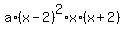 (1) (1)
with some unknown real coefficient  . .
To find  , use the fact that the plot of the polynomial goes through the point (5,252). It means that P(5) = 252. , use the fact that the plot of the polynomial goes through the point (5,252). It means that P(5) = 252.
So, simply substitute x=5 into the polynomial (1). You will get the equation
 = = 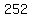 , or , or
 = = 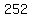 , or , or
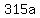 = = 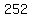 . .
Hence,  = = 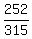 = =  . .
Therefore, P(x) =  . .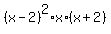 . .
You can open the parentheses if you need.
|
|
|