Question 994953: Find a polynomial f(x), that has the degree of 4 or less, so
f(−2) = 0, f(−1) = 0, f(0) = 0, f(1) = 9, f(2) = 0.
Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website! .
According to the condition, your polynomial has the roots -2, -1, 0, and 2.
Hence, the polynomial is
f(x) = a*(x-(-2))*(x-(-1))*(x-0)*(x-2) = a*(x+2)*x+1)*x*(x-2),
where a is a coefficient, an unknown real number.
To find a, use the condition f(1) = 9.
Simply substitute x=1 into this equation (into the polynomial). You will get
a*(1+2)*(1+1)*1*(1-2) = 9.
Simplify the left side. You will get a*3*2*1*(-1) = -6a.
So, the equation for a is
-6a = 9.
Hence, a =  =  .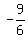
Now your polynomial is
f(x) = *(x+2)*x+1)*x*(x-2).
|
|
|
