.
x^2 + xy = 12, (1)
xy + y^2 = 6. (2)
Add two equations (1) and (2). You will get
 =
=  , or
, or  =
=  , or x + y = +/-
, or x + y = +/-  . (3)
Next, distract the equation (2) from the equation (1). You will get
. (3)
Next, distract the equation (2) from the equation (1). You will get
 =
=  , or (x+y)*(x-y) = 6. (4)
By combining (5) and (6), you have two linear systems of two equations in two unknowns
, or (x+y)*(x-y) = 6. (4)
By combining (5) and (6), you have two linear systems of two equations in two unknowns
 , and
, and  .
Simplify right sides:
.
Simplify right sides:
 , and
, and  .
First of these two systems has the solution x =
.
First of these two systems has the solution x = 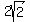 , y =
, y =  .
The second system has negative solutions x = -
.
The second system has negative solutions x = -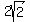 , y = -
, y = - .
According to the condition, only the pair x =
.
According to the condition, only the pair x = 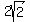 , y =
, y =  does suit.
does suit.