|
Question 993811: Find an equation for the line that is tangent to the circle x^2+y^2=169 at the point (5,12).
I need help beind reminded of the equation of a circle and equations related to this, and also a step-by-step explantion to help me to understand how to solve this typ of problems and others efficiently. Thank you so much!
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! Center of circle on the Origin,  , and for this, radius is r.
You have  , so the radius  .
The point ON THE CIRCLE, (5,12), is part of a tangent line which passes through this point. This means, you want to find an equation for this line and this line TOUCHES the circle at this point; and it is perpendicular to the line which contains this point (5,12) and the Origin (which is center of your circle.)
-
Work to understand that discussion before continuing.
What is the line containing the circle's center (0,0) and the given point (5,12)? You should find just intuitively this is  . The y-intercept and the x-intercept both 0.
What is the equation for the line PERPENDICULAR to and contains the point (5,12)? For perpendicularity, its slope must be negative reciprocal of  , so this slope needed will be 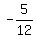 . You can use the point-slope equation form (for convenience if you are comfortable with it), and plug-in the needed slope and included point (5,12):
Use simple algebra if you want this equation in standard form or in slope-intercept form.
--
Try to make a sketch or a graph on your own to help analyze the problem description.
|
|
|
| |
