Question 993541: a motorboat maintained a constant speed of 15 miles per hour relative to the water in going 10 miles upstream and then returning. The total time for the trip was 1.5 hours. use this information to find the speed of the current.
Answer by ikleyn(52790)   (Show Source):
You can put this solution on YOUR website! .
A motorboat maintained a constant speed of 15 miles per hour relative to the water in going 10 miles upstream and then returning. The total time for the trip was 1.5 hours. use this information to find the speed of the current.
-----------------------------------------------------------------------
Let  be the unknown current speed of the river in miles per hour.
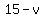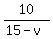When the motorboat moves upstream, its speed relative to the bank of the river is  miles per hour, and the time spent moving upstream is  hours.
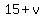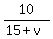When the motorboat moves downstream, its speed relative to the bank of the river is  miles per hour, and the time spent moving downstream is  hours.
So, the total time upstream and downstream is 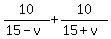 , and it is equal to 1.5 hours, according to the problem's input.
This gives an equation + =  .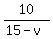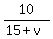
To simplify the equation, multiply both sides by  and collect like terms. Step by step, you get
 ,
 =  ,
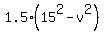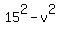 =  (after dividing both sides by 1.5),
 =  ,
=  ,
=  .
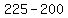Answer. The speed of the current is 5 miles per hour.
For more similar problems see the lesson Wind and Current problems solvable by quadratic equations in this site.
It is free of charge and without registration.
|
|
|
