|
Question 992821: Hi, I need help solving this : Find the point (x, y) on the line y=x that is equidistant from the points (8, 9) and (1, -10), thank you!
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
This point has coordinates (x,x) with the unknown x,
and the equation to find x is the equality of distances
from (x,x) to (8,9):  , and , and
from (x,x) to (1, -10): 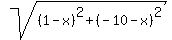 . .
This equation is (after squaring the square roots):
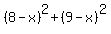 = = 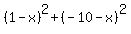 , or , or
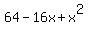 + + 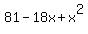 = = 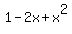 + + 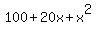 . .
Simplify and solve it.
64 + 81 -1 - 100 = 16x + 18x - 2x + 20x,
44 = 52x
x = 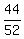 = =  . .
Answer. The point is ( , ,  ). ).
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you want to find the point on the line y = x that is the same distance from the points (8,9) and (1,-10).
that point will be (x,y) = (22/26, 22/26)
the following graph shows you where that point lies on the graph.

here's how you find it.
you need to find the equation of the line between the points (8,9) and (1,-10).
the equation of that line is y = 19/7 * x - 89/7.
you then need to find the midpoint of that line.
the midpoint of that line is (4.5, -1/2).
you then need to find the equation of a line perpendicular to the line of y = 19/7 * x - 89/7 and passing through the point (4.5, -1/2).
the equation of that line is y = -7/19 * x + 22/19.
that line is perpendicular to the line y = 19/7 * x - 89/7 because it's slope is the negative reciprocal of the slope of that line.
it doesn't look like it's perpendicular on the graph because i forgot to square the axes to make it look like what it is.
i'll correct that and show it to you again below after it's been squared.
that perpendicular line is the perpendicular bisector of the original line of y = 19/7 * x - 89/7.
any point on that line will be equidistant from the end points of that original line.
since that point needs to also intersect the line y = x, you need to find the intersection of the line y = x with the line y = -7/19 * x + 22/19.
that point is (22/26,22/26).
on the graph that shows up as .846 rounded to 3 decimal places, or .85 rounded to two decimal places.
following is the picture of the same graph after it was squared.
this picture clearly shows the perpendicularity.

i calculated the distance between the point (22/26,22/26) and the points (8,9) and (1,-10) and confirmed that the distances are the same.
|
|
|
| |