Question 992753: Given that cotx=-5/6 and x is in quadrant 2, find sin2x, cos2x,tan2x
Answer by ikleyn(52799)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Given that cotx=-5/6 and x is in quadrant 2, find sin2x, cos2x,tan2x
-------------------------------------------------------------------------
cot(x) = 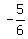 ---> ---> 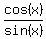 = = 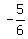 ---> --->  = = 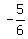 . . ---> --->
 = = 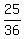 . . . (1) . (1)
 + +  = 1, (2) = 1, (2)
Now substitute (1) into (2). You will get
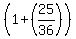 . . = 1, or = 1, or
 = =  = = 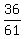 . .
Hence, sin(x) = 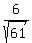 , cos(x) = - , cos(x) = -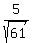 (taking into account that x is in the second quadrant). (taking into account that x is in the second quadrant).
Now, when you know sin(x) and cos(x) values, you can calculate the remaining functions.
Use the trigonometry formulas
sin(2x) = 2sin(x)*cos(x), = . . . ,
cos(2x) =  - -  = . . . , = . . . ,
and then tan(2x) = 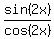 = . . . . = . . . .
Complete these calculations yourself.
Good luck!
|
|
|