|
Question 992626: Prove that n2 − 2 is not divisible by 5
Answer by ikleyn(52756)   (Show Source):
You can put this solution on YOUR website! .
Prove that  is not divisible by 5
--------------------------------------------------
For the proof let us represent the integer number n in the form
n = 5k + m, where 0 <= m < 5.
(m is the remainder after dividing n by 5. So m can take the values m = 0, 1, 2, 3 and 4 only).
Then
 =  =  =  ) +  .
First two addends are divisible by 5, so their sum is divisible by 5, too.
Hence, we need to check whether  is divisible by 5 for 5 values of m = 0, 1, 2, 3 and 4.
With m = 0  = -2 is not divisible by 5.
With m = 1 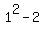 = -1 is not divisible by 5.
With m = 2  = 2 is not divisible by 5.
With m = 3  = 7 is not divisible by 5.
With m = 4 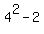 = 14 is not divisible by 5.
Hence, for any integer n, is not divisible by 5.
The proof is completed.
|
|
|
| |
