A tangent line can be thought of as a line that "intersects
a curve twice at the same point".
The value of y when x = 2 is



 So we want the equation of a tangent line at the point (2,10)
That is, we want to find the equation of the line through (2,10)
that is tangent to the parabola whose is equation is
So we want the equation of a tangent line at the point (2,10)
That is, we want to find the equation of the line through (2,10)
that is tangent to the parabola whose is equation is

 Let the tangent line have the equation
Let the tangent line have the equation
 The given equation of the parabola is
The given equation of the parabola is
 We set the two expressions for y equal to each other:
We set the two expressions for y equal to each other:


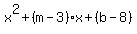 That quadratic will have a double solution if its
discriminant is 0
The discriminant is
That quadratic will have a double solution if its
discriminant is 0
The discriminant is  . We use capital
letters to distinguish little b and capital B.
. We use capital
letters to distinguish little b and capital B.

 Solve that for b
Solve that for b



 Substitute that for b in
Substitute that for b in

 And also the point (x,y) = (2,10)
And also the point (x,y) = (2,10)

 Multiply through by 4 to clear fraction:
Multiply through by 4 to clear fraction:





 Substitute this and (x,y) = (2,10) in
Substitute this and (x,y) = (2,10) in



 So the equation of the line is
So the equation of the line is
 So we draw that line on the graph to see if it looks like what we
have calculated. It has y-intercept and slope -1, and goes through
points (-1,13), (0,12), (4,8)
So we draw that line on the graph to see if it looks like what we
have calculated. It has y-intercept and slope -1, and goes through
points (-1,13), (0,12), (4,8)
 Edwin
Edwin