SOLUTION: Hello and thank you for your time. I have reviewed the same question, basically with different numbers, however I am not understanding how they are coming up with the solution. Any

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: Hello and thank you for your time. I have reviewed the same question, basically with different numbers, however I am not understanding how they are coming up with the solution. Any      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 992129: Hello and thank you for your time. I have reviewed the same question, basically with different numbers, however I am not understanding how they are coming up with the solution. Any help, (especially with explanation) will be much appreciated.
You are choosing between two health clubs. Club A offers a membership for a fee of $24 plus a monthly fee of $15. Club B offers a membership for a fee of $23 plus a monthly fee of $19. After how many months will the total cost of each health club be the same? What will be the total cost for each club?
Found 2 solutions by josgarithmetic, KMST:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
CLUB   MEMB.FEE   MONTHLY      COST for n months
A       24         15           15n+24
B       23         19           19n+23

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
x= number of month you are paying for a health club.
y= amount (in $) that you pay for the health club.
For Club A, what you pay can be calculated as
y=15x%2B24 .
For example, for 2 months you pay
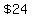2%2A%22%24+15%22=%22%2430%22 plus the %22%2424%22 premiership fee,
for a total (in $) of y=2%2A15%2B24=30%2B24=54 .
For Club B, what you pay can be calculated as
y=19x%2B23 .

With the numbers you give, he total cost of each health club will never be the same.
When you are assigned a problem like this in class, the numbers were calculated so as to give you reasonable answer, one that is a whole number of months.
With the numbers you give, if both costs were the same, you would have
19x%2B23=15x%2B24 ,
but that equation is only true for x=1%2F4 .
That means that the cost would be the same if you are a member for just 1%2F4 months.
However, x must be a whole number, because the clubs will nor charge you for fractions of a month.
If you do not withdraw from the club before the month begins, they will make you pay for the whole month, anyway, even if you tell them you don't want to be a member any more after one day of that month.

TO GET A BETTER IDEA OF HOW THIS KIND OF PROBLEM WORKS:
You can calculate for different values of x and make a table showing the cost for both clubs:
.
You can also make a graph with those numbers, plotting the points, and connecting them with a line:
It is hard to see in the graph, but the lines cross at a point with x=1%2F4 , and that (after 1%2F4 months) is where the cost would be the same for both clubs.

With the numbers you give, it is obvious that Club B is always more expensive than Club A,
and that the cost of Club B rises more steeply ($19 per month) compared to Club A ($15 per month).