|
Question 991812: a rectangle has a corner in quadrant 1 on the graph y=16-x^2, another at the origin, a third on the positive x-axis, and the fourth on the positive y- axis.
a. express the perimeter p of the rectangle as a function of x.
b. express the area as a function of x
c. what is the domain of A
could you please explain everything.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the perimeter of a rectangle is equal to 2*L + 2*W.
the area of a rectangle is equal to L * W.
L is the length of the rectangle (the horizontal sides).
W is the width of the rectangle (the vertical sides).
your rectangle has a corner in quadrant 1 on the graph of y = 16-x^2.
the (x,y) coordinates of that corner would be (x, 16-x^2).
you have another corner at the origin.
the (x,y) coordinate of that corner would be (0,0).
you have another corner on the positive x-axis.
the (x,y) coordinate of that corner would be (x,0).
you have another corner on the positive y-axis.
the (x,y) coordinate of that corner would be (0, 16-x^2).
a picture of your rectangle looks like this.
x can be any value between 0 and 4.
y can be any value between 0 and 16.
these are the limits because the line formed by the equation of y = 16 - x^2 has a y-intercept at y = 16 and has an x-intercept at x = 4.
the y-intercept is the value of y when x = 0.
when x = 0, y = 16 - x^2 becomes y = 16.
the x-intercept is the value of x when y = 0.
when y = 0, y = 16 - x^2 becomes 0 = 16 - x^2.
solve for x and you get x = 4.
i labeled your rectangle ABCD.
this makes your coordinates as follows:
A = (0,16-x^2)
B = (x, 16-x^2)
C = (x,0)
D = (0,0)
L is the length of your rectangle which is equal to the length of AB and is also equal to the length of DC because the length of AB and DC is the same in a rectangle.
W is the width of your rectangle which is equal to the length of AD and is also equal to the length of BC because the length of AD and BC is the same in a rectangle.
one of your coordinate points has to be (x,16-x^2) because that fixes that point to be on the line of y = 16-x^2.
this says that, if you want to find the length of L, you need to find the length of the line segment AB.
this also says that, if you want to find the length of W, you need to find the length of the line segment BC.
the pythagorean formula is used to find the length of a line segment.
by that formula, the length of a line segment is equal to
sqrt((x1-x2)^2 + (y1-y2)^2).
for the line segment of AB, you have:
x1 = 0 and x2 = x
y1 = 16-x^2 and y2 = 16-x^2
using the formula, you get:
L = length of AB = sqrt((x-0)^2 + ((16-x^2)-(16-x^2))^2).
simplify this to get L = sqrt (x^2 + 0^2)
simplify further to get L = sqrt(x^2).
this gets you L = x.
for the line segment of BC, you have:
x1 = x and x2 = x
y1 = 16-x^2 and y2 = 0
using the formula, you get:
W = length of BC = sqrt((x-x)^2 + ((16-x^2) - 0)^2).\
simplify this to get W = sqrt(0^2 + (16-x^2)^2).
simplify further to get W = sqrt((16-x^2)^2).
this gets you W = 16-x^2.
so you have:
L = x
W = 16-x^2
you're almost there.
perimeter (P)) of a rectangle = 2L + 2W which becomes P = 2x + 2(16-x^2).
area (A) of a rectangle = L 8 W which becomes A = x * (16-x^2)
The domain of A is the set of values of x that lead to a real solution.
x has to be greater than or equal to 0 because your rectangle has to be in quaderant 1.
x has to be less than or equal to 4 because it has to be contained within the confines of y = 16 - x^2 and the x-intercept of y = 16-x^2 is equal to 4.
the domain of A is therefore the set of all values of x such that x >= 0 and x <= 4.
you can pick any value of x greater than or equal to 0 and less than or equal to 4 and your rectangle will be within the confines of the x-axis and the y-axis and the line of y = 16 - x^2.
the graph of y = 16-x^2 is shown below:
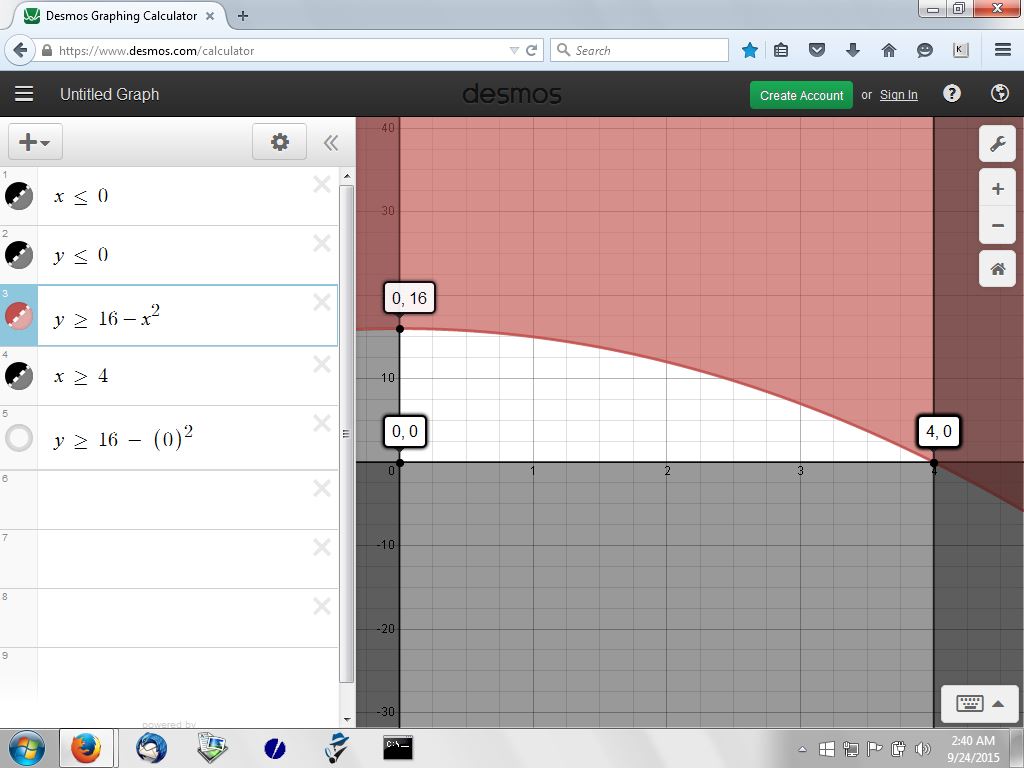
-----
the rectangle formed when x = 1 is shown below:

the length of the rectangle is equal to x which is equal to 1.
the width of the rectangle is equal to 16 - x^2 which is equal to 16 - 1^2 which is equal to 16 - 1 which is equal to 15.
P = 2L + 2W which is equal to 2*1 + 2*15 which is equal to 32 units.
A = L * W which is equal to 1*15 which is equal to 15 square units.
-----
the rectangle formed when x = 2 is shown below:

the length of the rectangle is equal to x which is equal to 2.
the width of the rectangle is equal to 16 - x^2 which is equal to 16 - 2^2 which is equal to 16 - 4 which is equal to 12.
P = 2L + 2W which is equal to 2*2 + 2*12 which is equal to 28 units.
A = L * W which is equal to 2*12 which is equal to 24 square units.
-----
the rectangle formed when x = 3 is shown below:

the length of the rectangle is equal to x which is equal to 3.
the width of the rectangle is equal to 16 - x^2 which is equal to 16 - 3^2 which is equal to 16 - 9 which is equal to 7.
P = 2L + 2W which is equal to 2*3 + 2*7 which is equal to 20 units.
A = L * W which is equal to 3*7 which is equal to 21 square units.
|
|
|
| |