Question 991505: Give an example for non zero real numbers is not closed under subtraction r
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! by definition, if the operation produces even one element outside of the set, the operation is  closed closed
set of natural numbers  is is  closed under subtraction closed under subtraction
example: let  and and  , then , then  => =>  is is  element of element of 
 is subset of the set of real numbers is subset of the set of real numbers 
note:
Real Numbers include:
Whole Numbers (like  , ,  , ,  , ,  , ,  , etc) , etc)
Rational Numbers (like  , , 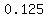 , , 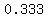 ..., ..., 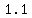 , etc ) , etc )
Irrational Numbers (like  , sqrt(3), etc ) , sqrt(3), etc )
One subset of Real Numbers is counting (or natural) numbers. This subset includes all the numbers we count with starting with " " to infinity. The subset would look like this: " to infinity. The subset would look like this:
{  , ,  , , , ,  , ,  ...} ...}
Another subset is whole numbers. This subset is exactly like the subset of counting numbers, with the addition of one extra number. This extra number is " ". The subset would look like this: ". The subset would look like this:
{  , ,  , ,  , , , ,  , ,  ...} ...}
so, your answer is set  or you can choose set of whole numbers or you can choose set of whole numbers
|
|
|