|
Question 990674: Consider the system −5x+2y−z = 0 and −5x−2y−z = 0. Both equations
equal zero and so −5x + 2y − z = −5x − 2y − z which is equivalent to y = 0. Does it follow that x and z can equal anything? Notice that when x = 1, z = −4, and y = 0 are plugged into the equations, the equations do not equal 0. Why?
Found 2 solutions by ikleyn, MathTherapy:
Answer by ikleyn(52898)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Hello,
1. Your conclusion that y=0 is correct.
2. For x and z we have only one equation (one constrain) 5x + z = 0.
It means that z can be anything, but x must be  . .
Or, in other words, x can be anything, but z must be 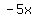 . .
Thank you for asking.
Answer by MathTherapy(10557)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Consider the system −5x+2y−z = 0 and −5x−2y−z = 0. Both equations
equal zero and so −5x + 2y − z = −5x − 2y − z which is equivalent to y = 0. Does it follow that x and z can equal anything? Notice that when x = 1, z = −4, and y = 0 are plugged into the equations, the equations do not equal 0. Why?
y is definitely 0, based on the elimination of the variables, x and z, when one of the equations is subtracted from the other.
One of the variables: x or z can be anything, but the other would be dependent on what that ANYTHING is.
For example, x can be any value, but then z would equal - 5 times that value of x, or  . .
Likewise, z can be any value, but then x would equal the negative value of z, divided by 5, or 
|
|
|
| |