|
Question 990624: Find the domain and range of the function:
f(x)=x^2+3x+10/x^2+6x+5
Answer by ikleyn(52788)   (Show Source):
You can put this solution on YOUR website! .
Find the domain and range of the function:  =  .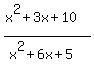
-----------------------------------------------------------------------------
The denominator is a quadratic polynomial. It has the roots -1 and -5. (You can find them using the quadratic formula or the Viete's theorem).
At these values of x the denominator is zero, so the function is not determined in these points. Therefore the domain is the entire number line except x=-1 and x=-5.
The numerator is again a quadratic polynomial, and it is always positive, since its discriminant d = b^2 - 4ac = 3^2 -4*1*10 = 9 - 40 = -31 is negative.
The denominator is negative inside the interval (-5, -1) and positive outside the segment [-5, -1].
From this, we can conclude that the given rational function is negative inside the interval (-5, -1) and is positive outside the segment [-5, -1].
Besides of it, the given rational function tends to - when x ---> (-5)+ and x ---> (-1)-.
At the same time the given rational function tends to when x ---> (-5)- and x ---> (-1)+.
The plot of the function is shown in the Figure below.
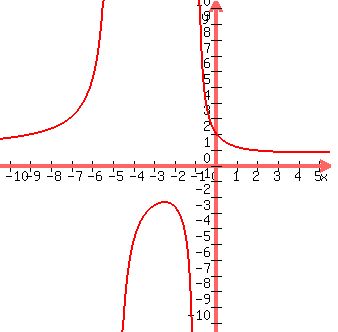
Figure.
|
It is predictable that the positive branches of the given rational function go from + to 1 when x ---> and x ---> -.
Thus the range includes the semi-infinite segment [1, ).
It also includes the semi-infinite segment [alpha, -) for some negative  .
To find the value of , we need to calculate the derivative f'(x) of the function and solve the equation f'(x) = 0.
It will be, actually, the equation for the numerator of the derivative, which would be again the quadratic polynomial.
But it is just too long way for me. Would you complete the solution and find the value of ?
|
|
|
| |
