Question 990562: The number of ways in which the number 27720 can be split into the product of two factors that are coprimes is
Answer by ikleyn(52830)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
27720 = 8*9*5*7*11
is the presentation of the number 27720 as the product of five co-prime numbers 8, 9, 5, 7, and 11.
So, we have basically 5 co-prime numbers, and the question is: in how many ways we can collect some of them into the first factor? (Then the rest of them will
automatically go into the second factor). The order of co-primes in the first factor does not make a difference. (Same as the order in the second factor does not).
It is the same as to ask: how many sub-sets is there in the set of 5 object?
The answer is:  . .
Indeed, the empty sub-set corresponds to the value 1 of the first factor.
The sub-sets consisting of 1 elements, give the values of 8, 9, 5, 7, and 11 for the first factor.
The sub-sets consisting of 2 elements give the factors 8*9, 8*5, 8*7, . . . , 7*11.
The sub-sets . . . . and so on.
Thus the number of ways in which we can construct the first factor is  . .
But since we do not make the difference between the first and the second factors, we need to divide this number by 2.
So, the answer is: The number of ways in which the number 27720 can be split into the product of two co-prime factors is 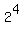 . .
|
|
|