SOLUTION: how many 5 element subsets can be found in Set (1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20)

Algebra ->  Subset -> SOLUTION: how many 5 element subsets can be found in Set (1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20)      Log On


   

Question 990553: how many 5 element subsets can be found in Set (1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20)
Found 2 solutions by farohw, ikleyn:
Answer by farohw(175) About Me  (Show Source):
You can put this solution on YOUR website!


S = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20}

C(20,5) = 20!/(20 - 5)!5!

= 20!/15!5!

= 2,432,902,008,176,640,000/(1,307,674,368,000)*(120)

= 15, 504 different 5 element subsets.


Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.
S = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20}

C(20,5) = 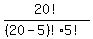20%21%2F%28%2820+-+5%29%215%21%29 = 20%21%2F%2815%215%21%29.

Actually,  you do not need to make long calculations.  Notice that

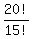20%21%2F15%21 = 16*17*18*19*20.

So,  the answer is

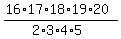20%21%2F%2815%215%21%29 = %2816%2A17%2A18%2A19%2A20%29%2F%282%2A3%2A4%2A5%29 = 2*17*6*19*4 =

= 15, 504 different 5 element subsets.