Question 989905: Norman has a dollar consisting of nickels, dimes and quarters. He has 2 ore dimes tan quarters and 6 more nickels than dimes. How many coins of each type does he have?
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39618)   (Show Source): (Show Source):
You can put this solution on YOUR website! n, d, q for nickels, dimes, quarters.

What to do, as a plan:
Simplify the money dollar equation to have whole number coefficients. Use the two coin relationship equations to make substitutions for d in the simplified money one dollar equation.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Norman has a dollar consisting of nickels, dimes and quarters. He has 2 ore dimes tan quarters and 6 more nickels than dimes. How many coins of each type does he have?
Let number of quarters be Q
Then number of dimes = Q + 2, and number of nickels = Q + 2 + 6, or Q + 8
The value equation, thus formed is: .25Q + .1(Q + 2) + .05(Q + 8) = 1
.25Q + .1Q + .2 + .05Q + .4 = 1
.25Q - .1Q + .05Q + .2 + .4 = 1
.4Q + .6 = 1
.4Q = 1 - .6
.4Q = .4
Q, or number of quarters = 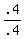 , or , or 
You should be able to find the number of dimes and nickels.
|
|
|