Question 989533: An airplane can travel 330 mph in still air. If it travels 2880 miles with the wind in the same length of time it travels 2400 miles against the wind, what is the speed of the wind?
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39618)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
An airplane can travel 330 mph in still air. If it travels 2880 miles with the wind in the same length of time it travels 2400 miles against the wind, what is the speed of the wind?
Let speed of wind be S
With the wind, the plane is going at a speed of: 330 + W
Against the wind, the plane is going at a speed of: 330 - W
We then get the following TIME equation: 
2,880(330 - W) = 2,400(330 + W) ------- Cross-multiplying
950,400 - 2,880W = 792,000 + 2,400W
- 2,880W - 2,400W = 792,000 - 950,400
- 5,280W = - 158,400
W, or speed of wind = 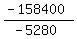 , or , or  mph mph
|
|
|