|
Question 988589: HI, this question is from my textbook.
The equations of two sides of a square are y=3x-1 and x+3y-6=0. (0,-1) is one vertex of the square. Find the coordinates of the other vertices.
Found 2 solutions by Alan3354, KMST:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! The equations of two sides of a square are y=3x-1 and x+3y-6=0. (0,-1) is one vertex of the square. Find the coordinates of the other vertices.
---------------
(0,-1) is point A.
Find the intersection of the lines, that's a 2nd vertex, point B.
---
y=3x-1
x+3y-6=0 --> y = (-1/3)x + 2
-----------
x + 3(3x-1) = 6
10x = 9
x = 0.9, y = 1.7 --> B(0.9,1.7)
-----------
The distance between the 2 points is the side length.
-----------
Find the line thru A(0,-1) parallel to x+3y-6=0
--> y = (-1/3)x - 1
A vertex (point D) is on this line distance s from point A.
The x-distance from A to D is 2.7, and the y-distance is 0.9
--> D (-2.7,-0.1)
------------------
The side CD goes thru D with a slope of 3 (parallel to AB)
y + 0.1 = 3(x + 2.7)
y = 3x + 8
---
Vertex C is the intersection of y = 3x + 8 and y = (-1/3)x + 2
3x + 8 = -x/3 + 2
10x/3 = -6
x = -1.8, y = 2.6
C(-1.8,2.6)
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website!  , and  are the equations of two sides of the square.
The coordinates of the vertex at the intersection of those two sides can be found by solving the system
 ---> ---> ---> ---> ---> ---> ---> .
So, point (9/10,17/10), or (0.9,1.7) is one vertex,
the one at the intersection of the two given sides.
Point (0,-1) , with  is the other end/vertex of that side with equation .
So far we have this:
What we do not know is to what side of segment 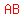 to draw the square.
There are really two right answers. Which one will be the right one according to your textbook? Or did the authors realize that there were two possible answers?
We can draw the square to the right, like this:
 , or we can draw the square to the left, as Alan suggested.
Either way, if we encase that square inside a larger square with sides parallel to the x- and y-axes,
we form four congruent right triangles with legs measuring
 and  , like this 
So,  ,  ,
 , and  .
|
|
|
| |
