|
Question 987825: Please help me understand how to determine if these pairs of lines are perpendicular parallel or neither:
1. y = 4/3
2. -4x = 3
3. x = 4/3
Found 2 solutions by ikleyn, MathLover1:
Answer by ikleyn(52784)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1. y = 4/3. It is horizontal line parallel to the x-axis.
2. -4x = 3. It is vertical line parallel to the y-axis.
3. x = 4/3. It is vertical line parallel to the y-axis.
So, the line "1" is perpendicular to lines "2" and "3".
The line "2" is parallel to the line "3".
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! First, put all equations in the "slope-intercept" form: 
If two lines are perpendicular, their slopes are the negative reciprocal of each other.
If two lines are parallel, their slopes are same.
If the slope values are not the same, so the lines are not parallel.
If the slope values are not negative reciprocals either, so the lines are not perpendicular. Then the answer is "neither".
you are given:
1.  .....eq.1 .....eq.1
2.  .....eq.2 .....eq.2
3.  ......eq.3 ......eq.3
put all equations in the "slope-intercept" form
1.  .....eq.1=> slope is .....eq.1=> slope is  , y-intercept is , y-intercept is  ; so, this line is a horizontal line that intercept y-axis at ; so, this line is a horizontal line that intercept y-axis at 
2.  .....eq.2 => .....eq.2 =>  => => => => , the line is vertical and slope is , the line is vertical and slope is  , x-intercept is , x-intercept is  ; ;
3.  ......eq.3=> ......eq.3=> , the line is vertical and slope is , the line is vertical and slope is  , x-intercept is , x-intercept is 
so, line 1 (which is horizontal line) and 2 (which is vertical line) are 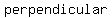 to each other to each other
so, line 1 (which is horizontal line) and 3 (which is vertical line) are 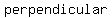 to each other to each other
so, line 2 (which is vertical line) and 3 (which is vertical line) are 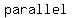 to each other to each other

|
|
|
| |