SOLUTION: a) Is y = x^2 + 7x + 12 a quadratic equation*? Why or why not? b) Can it be solved by factoring? If yes, solve it. If not, why not? c) As it happens, the equation y = x^2 + 3

Algebra ->  Quadratic Equations and Parabolas -> SOLUTION: a) Is y = x^2 + 7x + 12 a quadratic equation*? Why or why not? b) Can it be solved by factoring? If yes, solve it. If not, why not? c) As it happens, the equation y = x^2 + 3      Log On


   

Question 986721: a) Is y = x^2 + 7x + 12 a quadratic equation*? Why or why not?
b) Can it be solved by factoring? If yes, solve it. If not, why not?
c) As it happens, the equation y = x^2 + 3x - 23 also cannot be solved by factoring. One method of solving quadratic equations, however, that will solve ALL of them, is called using the quadratic formula. Can you state and explain the quadratic formula?
d) Use the quadratic formula to solve y = x^2 + 3x - 23 and explain your steps.
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
a) Is y = x^2 + 7x + 12 a quadratic equation*? Why or why not?
Yes, it is. There's an x^2 term and no other 2nd order terms.
=================
b) Can it be solved by factoring? If yes, solve it. If not, why not?
Yes, it can.
You factor it, I don't need the practice.
======================
c) As it happens, the equation y = x^2 + 3x - 23 also cannot be solved by factoring. One method of solving quadratic equations, however, that will solve ALL of them, is called using the quadratic formula. Can you state and explain the quadratic formula?
Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B3x%2B-23+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%283%29%5E2-4%2A1%2A-23=101.

Discriminant d=101 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-3%2B-sqrt%28+101+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%283%29%2Bsqrt%28+101+%29%29%2F2%5C1+=+3.52493781056044
x%5B2%5D+=+%28-%283%29-sqrt%28+101+%29%29%2F2%5C1+=+-6.52493781056044

Quadratic expression 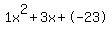1x%5E2%2B3x%2B-23 can be factored:
1x%5E2%2B3x%2B-23+=+1%28x-3.52493781056044%29%2A%28x--6.52493781056044%29
Again, the answer is: 3.52493781056044, -6.52493781056044. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B3%2Ax%2B-23+%29

The online solver ALWAYS says it can be factored. Ignore that.
=======================
d) Use the quadratic formula to solve y = x^2 + 3x - 23 and explain your steps.
See above.