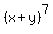SOLUTION: What is the coefficient of {{{x^3y^4}}} in the binomial expansion of {{{(x+y)^7}}}? Thank you kindly.

For this problem, the formula to determine a specific term in a Bernoulli/Binomial expansion should be used. It states:

, where r = term number 



We have: , which becomes: 

The expression: , without its coefficient, occurs at the term where 

Thus, 3 = 7 - (r - 1)

3 = 7 - r + 1

3 = 8 - r

3 - 8 = - r 

- 5 = - r

r, or term number where  occurs = , or 5 



Confirming this, and as seen above, 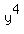 occurs at , and so:

4 = r - 1

4 + 1 = r

r, or term number where 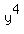 occurs = 5 



This means that the expression:  without its coefficient occurs at the 5th term



We now have: 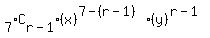, with r or term number being 5

This becomes: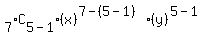  

 





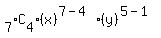
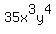
As seen the coefficient of  in the expansion of:  is: