|
Question 986202: twice the middle digit of a three- digit number is the sum of the other two. if the no. is divided by the sum of its digit, the answer is 56 and the remainder is 8. If the digits are reversed, the number becomes smaller by 594. Find the no.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Spent a lot of time on this problem, unable to get integer solution when the remainder is 8, changing the remainder to 12 will solve it
let a = the 100's digit
let b = the 10's digit
let c = the units
:
Write an equation for each statement
:
twice the middle digit of a three-digit number is the sum of the other two.
2b = a + c
:
if the no. is divided by the sum of its digit, the answer is 56 and the remainder is 12.
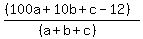 = 56 = 56
here we can replace a+c with 2b from the 1st statement, so we have
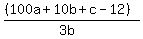 = 56 = 56
100a + 10b + c - 12 = 56(3b)
100a + c = 168b - 10b + 12
100a + c = 158b + 12
:
If the digits are reversed, the number becomes smaller by 594.
100c + 10b + a = 100a + 10b + c - 594
Combine like terms
100c - c + 10b - 10b = 100a - a - 594
99c = 99a - 594
simplify divide by 99
c = a - 6
:
Back to the first equation 2b = a + c, replace c with a-6
2b = a + a - 6
2b = 2a - 6
Simplify, divide by 2
b = a - 3
:
Back to the 2nd eq: 100a + c = 158b + 12, replace b with (a-3), c with (a-6)
100a + (a-6) = 158(a-3) + 12
101a = 158a - 474 + 12 + 6
101a - 158a = -474 + 18
57a = 456
a = 456/57
a = 8 is the first digit
then
b = 8 - 3
b = 5
and
c = 8 - 6
c = 2
:
Find the no. 852
:
You can check this for yourself in each statement.
|
|
|
| |