Question 986181: Three roots of a fourth-degree polynomial equation with rational coefficients are 5+√3, –17, and 2-√4. Which number also is a root of the equation?
A. 17
B. 2+√4
C. 4-√2
D. 5-√3
How does this make sense? I thought that if you switched the addition/subtraction symbol, then you will have the other root. So shouldn't A, B, and D all be correct?
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Since  , we know that , we know that  . They made this root a bit more complicated than it had to be to confuse you. The three roots, as simple as they can get, are given as . They made this root a bit more complicated than it had to be to confuse you. The three roots, as simple as they can get, are given as 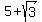 , , 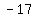 , and , and 
Rule: if you have a polynomial with rational coefficients, and you have a root 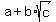 , then , then 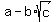 must also be a root as well. must also be a root as well.
So if 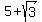 is a root, then is a root, then  must also be a root (note: a = 5, b = 1, c = 3 in this case) must also be a root (note: a = 5, b = 1, c = 3 in this case)
Final Answer: Choice D) 
|
|
|