Question 986161: Find the values of a, b, and c such that the equation y = ax2 + bx + c has ordered pair solutions (-1, -4), (2, -7) and (3, 0)
this is just a pretest
Found 3 solutions by stanbon, solver91311, MathLover1:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the values of a, b, and c such that the equation y = ax2 + bx + c has ordered pair solutions (-1, -4), (2, -7) and (3, 0)
this is just a pretest
------
Form:: ax^2 + bx + c = y
Solve for a,b, and c using the 3 pairs::
a - b + c = -4
4a +2b + c = -7
9a +3b + c = 0
----------------------
Using any method you know solve for a, b, and c::
Ans::
a = 2 ; b = -3 ; c = -9
-----
Equation:
y = 2x^2 -3x - 9
======================
Cheers,
Stan H.
---------------
Answer by solver91311(24713)   (Show Source): (Show Source):
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the values of  , ,  , and , and  such that the equation such that the equation  has ordered pair solutions ( has ordered pair solutions ( , ,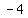 ), ( ), ( , , ) and ( ) and ( , , ): ):
for ( , , )=( )=( , ,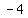 ) )

 .............eq.1 .............eq.1
for ( , , )= ( )= ( , , ) )

 .............eq.2 .............eq.2
for ( , , )=( )=( , , ) )

 .............eq.3 .............eq.3
solve this system:
 .............eq.1 .............eq.1
 .............eq.2 .............eq.2
 .............eq.3 .............eq.3
------------------------------------------------
start with
 .............eq.1 .............eq.1
 .............eq.2...subtract 1 from 2 .............eq.2...subtract 1 from 2
-----------------------------------




 .............eq.1a .............eq.1a
go with
 .............eq.2 .............eq.2
 .............eq.3..........subtract 2 from 3 .............eq.3..........subtract 2 from 3
--------------------------------------------


 ..........eq.2a ..........eq.2a
from eq.1a and 2a we have
 ........solve for ........solve for 




go to
 .............eq.1a.....substitute .............eq.1a.....substitute  for for 



go to  .............eq.3 ...substitute .............eq.3 ...substitute  for for  , , for for 




so, your equation is: 

|
|
|