Question 985625: Factor the polynomial P(x). Then solve the equation P(x)=0.
1.P(x)=x^3+4x^2+x-6
2.P(x)=x^3-6x^2-x+6
3.P(x)=x^3-x^2-x+1
4.P(x)=2x^3-3x^2-3x+2
Answer by ikleyn(52771)   (Show Source):
You can put this solution on YOUR website!
Factor the polynomial P(x). Then solve the equation P(x)=0.
1. P(x) = 
2. P(x) = 
3. P(x) =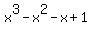 
4. P(x) = 
----------------------------------------------------------
1. P(x) =  .
The integer 1 is the root. Indeed, P(1) =  =  =  .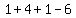
It means that the binomial (x-1) divides the polynomial P(x): P(x) = (x-1)*Q(x), where Q(x) is a quadratic polynomial. (See the Remainder Theorem in the lesson
Divisibility of polynomial f(x) by binomial x-a in this site).
If you make the long division, you will get Q(x) =  .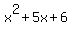
The quadratic polynomial Q(x) has the roots -2 and -3: Q(-2) = 0 and Q(-3) = 0.
You can use the quadratic formula to find the roots (see the lesson Introduction into Quadratic Equations in this site) or
the Vieta's Theorem (see the lesson Solving quadratic equations without quadratic formula). You also can check it directly.
This means that the binomials (x+2) and (x+3) divide the polynomial Q(x), so Q(x) = (x+2)*(x+3).
You also can check this factorization immediately.
It implies that the polynomial P(x) has the factorization P(x) = (x-1)*(x+2)*(x+3).
Hence, its roots are 1, -2 and -3.
2. P(x) =  .
Re-group: P(x) =  -  =  =  = (x-6)*(x-1)*(x+1).
The roots of the polynomial P(x) are 6, 1 and -1.
3. P(x) =  .
Re-group: P(x) =  -  =  =  = (x-1)*(x-1)*(x+1).
The roots of the polynomial P(x) are 1 (multiplicity 2), and -1.
4. P(x) =  .
One root is 2: P(2) = 0 (check it yourself).
Hence, P(x) is divided by (x-2): P(x) = (x-2)*Q(x), where Q(x) is a quadratic polynomial. (By the same reason as in the n.1 above).
Long division gives Q(x) =  .
Hence, P(x) =  .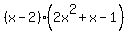
The quadratic polynomial has the roots -1 and  . You can find them using the same methods as in the n.1 above.
So, Q(x) = =  .
Thus P(x) = 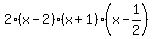 is the final factorization of the polynomial P(x) over the real domain.
The polynomial P(x) has the roots 2, -1 and .
|
|
|
