|
Question 985482: For the circle  and the line and the line  , determine the exact values of the gradient , determine the exact values of the gradient  so that the line: so that the line:
a) is a tangent to the circle
b) intersects the circle in two places
c) does not intersect the circle
Found 3 solutions by KMST, solver91311, ikleyn:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  gives us the intersection points of circle and line. gives us the intersection points of circle and line.
 ---> ---> ---> ---> ---> --->
That is a quadratic equation.
A quadratic equation of the form 
has no real solutions if 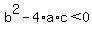 . .
It has one real solution if  , and , and
it has two real solutions if  . .
For the quadratic equation  , ,  ,so ,so
 . .
The zeros of 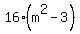 are the zeros of are the zeros of 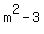 , given by , given by
 and and  . .
For those values, the line is tangent to the circle.

In between those values of  , ,
for 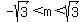 , ,
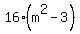 is negative, and the line does not intersect the circle. is negative, and the line does not intersect the circle.
Otherwise, for 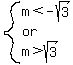 , ,
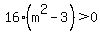 , and the line intersects the circle in two places. , and the line intersects the circle in two places.
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website!
KMSTs solution is more general, and therefore better, IMHO, than what I am about to show you. However, this is a slightly different way to look at this particular problem and may give you some additional insight.
Note that a tangent to a circle is perforce perpendicular to a radius. An examination of the diagram shows us that a tangent as described, the perpendicular radius, and that segment of the  -axis between the origin and the -axis between the origin and the  -intercept of the desired line form a right triangle. Since the measure of the radius of the circle which forms the short leg of the right triangle is 2 and the measure of the -intercept of the desired line form a right triangle. Since the measure of the radius of the circle which forms the short leg of the right triangle is 2 and the measure of the  -axis segment that forms the hypotenuse of the right triangle measures 4, we have a 30-60-90 right triangle, where the angle between the radius and the -axis segment that forms the hypotenuse of the right triangle measures 4, we have a 30-60-90 right triangle, where the angle between the radius and the  axis is the 60 degree angle. See figure below: axis is the 60 degree angle. See figure below:
 . .
That means that the angle between the radius ray and the  -axis is 30 degrees. A quick examination of a unit circle and using a multiplier of 2 to match the radius of the given circle, we see readily that the point of tangency in QI is -axis is 30 degrees. A quick examination of a unit circle and using a multiplier of 2 to match the radius of the given circle, we see readily that the point of tangency in QI is ) . .
Using the slope formula, the slope of the line that passes through the points ) and and ) is is  . .
Symmetry gives us a second point of tangency in QII, which is simply ) and then the slope of the line through the second point is just the additive inverse of the slope of the first equation. and then the slope of the line through the second point is just the additive inverse of the slope of the first equation.
From there it should be clear that any slope in the open interval ) will produce a secant line. will produce a secant line.
Further, any slope in either open interval ) or or ) will produce a line that does not intersect the circle. will produce a line that does not intersect the circle.
John

My calculator said it, I believe it, that settles it

Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website!
To find the intersection points of the circle and the straight line, substitute  = = 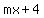 into the equation into the equation  = =  . You will get . You will get
 + + 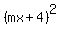 = =  , ,
 + + 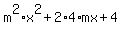 = =  , ,
 = =  , ,
 = =  . .
Next, apply the quadratic formula to find the roots
 = = 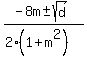 , ,
where  is the discriminant is the discriminant  = = 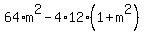 = = 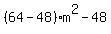 = = 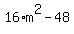 . .
Now everything is determined by the discriminant.
If  > >  , then there are two roots. Correspondingly, there are two intersection points. , then there are two roots. Correspondingly, there are two intersection points.
In opposite, if there are two intersection points, then there are two roots, hence,  > >  . .
If  = =  , then there is only one root. It means that the straight line tangents the circle. , then there is only one root. It means that the straight line tangents the circle.
And in opposite, if the straight line tangents the circle, then there is only one root, hence,  = =  . .
Finally,  < <  <-----> there are no intersection points. <-----> there are no intersection points.
Thus you need to solve this critical equation
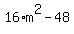 = =  . .
It gives
 = +/- = +/-  . .
So, if  = +/- = +/-  , then the straight line tangents the circle. , then the straight line tangents the circle.
If  > >  , then , then  > > and there are two intersection points. and there are two intersection points.
If  < <  < <  , then , then  < < and there are no intersection points. and there are no intersection points.
|
|
|
| |