Question 985414: Alice is charging her phone and tablet at the same time. The phone has 15% of a charge left and charges at a rate of 8% every 10 minutes. The tablet has a 25% charge left and charges at a rate of 15% every 30 minutes.
Write a system of equations to represent this situation:
Phone Charge:_______________ Tablet Charge:________________
What do the variables represent? ______________________
Solve this system of equations and show your work.
When will the phone and tablet have the same charge? ________% / _______mins
How long will it take for the phone to be fully charged? ________mins
How long will it take for the tablet to be fully charged? _________mins
THANK YOU SO MUCH IF U CAN FIGURE THIS OUT, ITS INTEGRATED MATH I QUESTION 💖💖💖👍👍👍
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website!
In my view, the presented formulation is ambiguous, and it is the major obstacle in solving it.
As I understand the situation, there is the phone with the present charge equal to 0.15 of its full charge capacity.
It is charging at the rate of 0.08 of its full charge capacity each 10 minutes.
On the other side, there is the tablet, whose present charge is 0.25 of its full charge capacity.
It is charging at the rate of 0.15 of its full charge capacity each 30 minutes.
Actually, it is a typical problem on "Travel and Distance". You have the initial position, the rate, the distance, and you need to find the time.
For the phone, let p be the phone current charge during the charging process, measured in units of its full capacity (in "percentage", if you want).
Then the model equation for the phone charging process is
 = =  + +  , (1) , (1)
where t is time in minutes.
For the tablet, let s be the tablet current charge during the charging process, measured in units of its full capacity.
Then the model equation for the tablet charging process is
 = =  + + 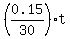 , (2) , (2)
where t is time in minutes.
Now, let us answer the question:
How long will it take for the phone to be fully charged?
To answer it, we should solve the equation p = 1, which takes the form
 + +  = =  , (3) , (3)
in accordance with (1).
Should I continue or everything is just clear to you?
|
|
|