SOLUTION: {{{tan(A)=2/3}}} A ∈ QIII, {{{sec(B)=3}}} B ∈ QI find {{{cos(A+B)}}}

.

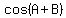
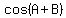
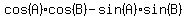First we draw the two angles, A, B, in their respective quadrants:

 
Draw perpendiculars to the x-axis from the end of the terminal sides of
the angles, creating right triangles.

 

For angle A:
. Since the adjacent side, x, goes left
on the x-axis, and the opposite side, y, goes downward from the x-axis, we must
consider the tangent  as 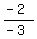 and put the numerator of ,
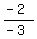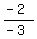which is -2, on the y=OPPOSITE side and the denominator of , which is
-3, on the x=ADJACENT SIDE.

For angle B:
Since  is in QI we can leave everything positive.
We put the numerator of 3/1, which is 3, on the r=HYPOTENUSE and the denominator
of 3/1, which is 1, on the x=ADJACENT SIDE. 

Then we calculate the third sides of the two right triangles by using the
Pythagorean theorem:  

for angle A:                  for angle B:
                                          
              
                      
                       
                      
                            
                            

 

Now we are able to substitute in

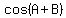
 and 









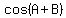
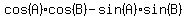
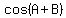
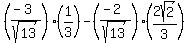
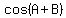
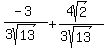
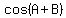
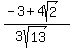Rationalizing the denominator:







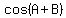
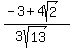
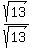
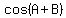
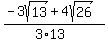
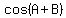
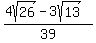Edwin