Question 985138: Pleaaaase help i really need some one to properly walk through this all. Thank you soooo much !!!!!
At most how many solutions can a quadratic equation have? Give an example of a quadratic equation that has two solutions and show those solutions. Give an example of a quadratic equation that has only one solution and show that solution. Give an example of a quadratic equation that has no solution and explain what that means. Based on thus work, give your definition of the solution of a quadratic equation.
Answer by josgarithmetic(39615)   (Show Source): (Show Source):
You can put this solution on YOUR website! How many solutions depends how you have the equation.
y=f(x), then infinitely many solutions.
y=0, may have none, exactly one, or exactly two real solutions.
Anything in the form f(x)=a(x-h)^2+k or f(x)=ax^2+bx+c will have infinitely many solutions. Same as if y=a(x-h)^2+k or y=ax^2+bx+c. Parabolas - many points, all forming the shape.
Something in the form a(x-h)^2+k=0 or ax^2+bx+c=0 Might or might not yield, at least temporarily until further steps, an irrational expression which may contain negative value (no real solutions), positive value (two real solutions) or be zero (and just touches x-axis with the parabola's vertex, meaning ONE real solution).
If you are really interested in the type of equation like  , then maybe this will reenforce what was said: , then maybe this will reenforce what was said:
Starting with any quadratic expression in one variable, you can obtain or be given standard form  , and solve this for x. , and solve this for x.
-
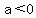 OR OR  ; ;
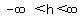 ; ;
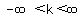
-



 ------understand very clearly, this does not say that ------understand very clearly, this does not say that 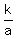 is negative and it does not say that is negative and it does not say that 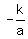 is negative. k and a maybe be positive or negative in any combination by itself. is negative. k and a maybe be positive or negative in any combination by itself.
What is important is the kind of value of 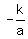 . IF negative, then no real solution, because it is held inside the square root function, so only square roots of positive values have real values. IF . IF negative, then no real solution, because it is held inside the square root function, so only square roots of positive values have real values. IF 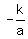 positive, then TWO real solutions, because you have something that can be PLUSED to yield an x, and something that can be MINUSED to yield the other x, solution. If positive, then TWO real solutions, because you have something that can be PLUSED to yield an x, and something that can be MINUSED to yield the other x, solution. If 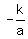 is 0, then you simply have is 0, then you simply have  which is which is  , just one single solution. , just one single solution.
|
|
|