Question 984773: x^2=y+z, y^2=z+x, z^2=x+y, then what is the value of (1/(x+1)) + (1/(y+1)) + (1/(z+1))?
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
x²=y+z, y²=z+x, z²=x+y
The three equations are symmetrical,
so anything we discover about any pair
of variables, it will also be true of any
other pair of variables.
Solve the first two for z.
x²-y=z y²-x=z
x²-y = y²-x, since both equal to z
x²-y² = -x+y
(x-y)(x+y) = -(x-y)
We will see if we can divide by x-y
We will first assume x-y ≠ 0. Then we can divide both
sides by x-y and get
x+y = -1
But since z²=x+y, then that would
mean z²=-1 and z would be ±i.
Then by the symmetry x and y would
also be ±i but then x²=y+z would give
-1=i+i, -1=i-i, -1=-i+i or -1=-i-i,
none of which are possible.
Therefore we cannot divide both sides of
(x-y)(x+y) = -(x-y)
by x-y, and therefore the assumption x-y≠0
was false and therefore x-y=0 and x=y.
By symmetry x=y=z, so all three equations
amount to
x²=x+x
x²=2x
x²-2x = 0
x(x-2) = 0
x=0, x=2
By symmetry then x=y=z=0 or x=y=z=2
If x=y=z=0 then
 = =
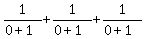 = =
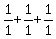 = = 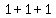 = 3
If x=y=z=2 then = 3
If x=y=z=2 then
 = =
 = =
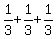 = 1
Answer: 3 or 1
Edwin = 1
Answer: 3 or 1
Edwin
|
|
|