SOLUTION: A piece of work can be done by 6 men and 5 women in 6 days or 3 men and 4 women in 10 days.In how many days can be done by 9 men and 15 women?

Algebra ->  Rate-of-work-word-problems -> SOLUTION: A piece of work can be done by 6 men and 5 women in 6 days or 3 men and 4 women in 10 days.In how many days can be done by 9 men and 15 women?      Log On


   

Question 984757: A piece of work can be done by 6 men and 5 women in 6 days or 3 men and 4 women in 10 days.In how many days can be done by 9 men and 15 women?
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52754) About Me  (Show Source):
You can put this solution on YOUR website!

Let assume that all men have the same rate of work,  and all women have the same rate of work,  perhaps,  different from  (or distinct of)  the men's rate of work
(for example,  it is so in the typing work;  or in the moving of heavy objects.  At least,  we can think/imagine that it is true :)

Let in this scheme  m  be the the man's rate of work,  and let  w  be the woman's rate of work.

Then we have the linear system of two equations in two unknowns,  in accordance with the given data:

system%286%2A%286m+%2B+5w%29+=+1%2C%0D%0A10%2A%283m+%2B+4w%29+=+1%29,

or

system%2836m+%2B+30w+=+1%2C%0D%0A30m+%2B+40w+=+1%29.

To solve it,  subtract the second equation of the last system from the first equation.  You will get

6m = 10w,     or     w = 6%2F10m = 3%2F5m.

Next,  substitute it into the first equation of the system,  and you will get

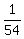w = 1%2F90,   and then   m = 1%2F54.

Very good.  Now,  calculate the value of the expression   9m + 15w,   which is the subject of the problem's question.  It is

9m + 15w = 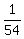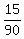9.1%2F54 + 15.1%2F90 = 9%2F54 + 15%2F90 = 1%2F6 + 1%2F6 = 1%2F3.

Hence,  9  men and  15  women will complete the work in  3  days.


Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
A piece of work can be done by 6 men and 5 women in 6 days or 3 men and 4 women in 10 days.In how many days can be done by 9 men and 15 women?

>>A piece of work can be done by 6 men and 5 women in 6 days...
Suppose a man's work rate in jobs per day is 1 job per M days, or 1/M jobs per day.

Suppose a woman's work rate in jobs per day is 1 jobs per W days, or 1/W jobs per day.

In 6 days 1 man can do (1/M)*6 = 6/M (fraction of a job)
In 6 days 1 woman can do (1/W)*6 = 6/W (fraction of a job)

Therefore:

In 6 days 6 man can do 6*6/M jobs or 36/M (fraction of a job).
In 6 days 5 women can do 5*6/W jobs or 30/W (fraction of a job).

So in those 6 days they did 36/M+30/W which equals 1 job:

So one equation is 36/M + 30/W = 1

>>or 3 men and 4 women in 10 days.
Therefore

In 10 days 3 man can do 3*10/M jobs or 30/M (fraction of a job).
In 10 days 4 women can do 4*10/W jobs or 40/W (fraction of a job).

So in those 10 days they did 30/M+40/W which equals 1 job:

So another equation is 30/M + 40/W = 1

The system is

system%2836%2FM+%2B+30%2FW+=+1%2C30%2FM+%2B+40%2FW+=+1%29

It makes a mess to clear of fractions, so don't!

Use elimination.  Multiply the first equation by 4 and the second
by -3 to cancel the W terms:

system%28144%2FM+%2B+120%2FW+=+4%2C-90%2FM+-+120%2FW+=+-3%29

54%2FM=1

54=M

So 1 man can do the job in 54 days.

Substitute in 36%2FM+%2B+30%2FW+=+1
              36%2F54+%2B+30%2FW+=+1
              2%2F3+%2B30%2FW+=+1

Now we can clear of fractions:

              2W%2B90=3W
              90=W

So 1 woman can do the job in 90 days.

>>In how many days can be done by 9 men and 15 women?

In 1 day 9 men can do 9/M=9/54=1/6 (fraction of a job).
In 1 day 15 women can do 15/W=15/90=1/6 (fraction of a job).

So together in one day they can do 1/6+1/6 = 2/6 = 1/3 of a job.

So it will take them 3 days

Edwin