|
Question 98453: These 3 problems do not come from a book but I really need help with them!
If you can solve them as soon as possible, I would greatly appreciate it.
Here they are:
#1:
Write the equation of the line passing through the points listed below. Write the final answer in the slope-intercept form y = mx + b. If the slope (m) or the y-intercept (b) are not integers, fractions must be used.
(-1, 8); (9, 2)
#2:
A line passes through the origin and the point (-6, 4).
Write the equation of the line that passes through (-6, 4) and is perpendicular to the given line.
Write the final answer in the slope-intercept form y = mx + b.
(The slope and y-intercept must be written as fractions, when needed).
#3:
Write the equation for the line perpendicular to
2x - 5y = 5 and passes through the point (-2, -5).
Enter the variable expression Ax + By separately from the constant term C.
Your response should be given in standard form where A, B and C are the smallest possible integers and A > 0.
Thanks so much.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! These explanations are quite lengthy, so here's a mini table of contents
#1
#2
#3
Go to top
"#1:
Write the equation of the line passing through the points listed below. Write the final answer in the slope-intercept form y = mx + b. If the slope (m) or the y-intercept (b) are not integers, fractions must be used.
(-1, 8); (9, 2)"
First lets find the slope through the points ( , , ) and ( ) and ( , , ) )
 Start with the slope formula (note: Start with the slope formula (note: ) is the first point ( is the first point ( , , ) and ) and ) is the second point ( is the second point ( , , )) ))
 Plug in Plug in  , , , , , , (these are the coordinates of given points) (these are the coordinates of given points)
 Subtract the terms in the numerator Subtract the terms in the numerator 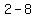 to get to get  . Subtract the terms in the denominator . Subtract the terms in the denominator 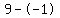 to get to get 
 Reduce Reduce
So the slope is

------------------------------------------------
Now let's use the point-slope formula to find the equation of the line:
------Point-Slope Formula------
 where where  is the slope, and is the slope, and ) is one of the given points is one of the given points
So lets use the Point-Slope Formula to find the equation of the line
 Plug in Plug in  , ,  , and , and  (these values are given) (these values are given)
 Rewrite Rewrite  as as 
 Distribute Distribute 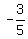
 Multiply Multiply 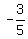 and and  to get to get 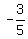
 Add Add  to both sides to isolate y to both sides to isolate y
 Combine like terms Combine like terms 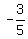 and and  to get to get 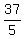 (note: if you need help with combining fractions, check out this solver) (note: if you need help with combining fractions, check out this solver)
------------------------------------------------------------------------------------------------------------
Answer:
So the equation of the line which goes through the points ( , , ) and ( ) and ( , , ) is: ) is:
The equation is now in  form (which is slope-intercept form) where the slope is form (which is slope-intercept form) where the slope is  and the y-intercept is and the y-intercept is 
Notice if we graph the equation  and plot the points ( and plot the points ( , , ) and ( ) and ( , , ), we get this: (note: if you need help with graphing, check out this solver) ), we get this: (note: if you need help with graphing, check out this solver)
 Graph of Graph of  through the points ( through the points ( , , ) and ( ) and ( , , ) )
Notice how the two points lie on the line. This graphically verifies our answer.
Go to top
#2:
"A line passes through the origin and the point (-6, 4).
Write the equation of the line that passes through (-6, 4) and is perpendicular to the given line.
Write the final answer in the slope-intercept form y = mx + b.
(The slope and y-intercept must be written as fractions, when needed). "
First find the equation of the line through the points (0,0) (the origin) and (-6,4)
First lets find the slope through the points ( , , ) and ( ) and ( , , ) )
 Start with the slope formula (note: Start with the slope formula (note: ) is the first point ( is the first point ( , , ) and ) and ) is the second point ( is the second point ( , , )) ))
 Plug in Plug in  , , , , , , (these are the coordinates of given points) (these are the coordinates of given points)
 Subtract the terms in the numerator Subtract the terms in the numerator 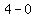 to get to get  . Subtract the terms in the denominator . Subtract the terms in the denominator 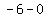 to get to get 
 Reduce Reduce
So the slope is

------------------------------------------------
Now let's use the point-slope formula to find the equation of the line:
------Point-Slope Formula------
 where where  is the slope, and is the slope, and ) is one of the given points is one of the given points
So lets use the Point-Slope Formula to find the equation of the line
 Plug in Plug in  , ,  , and , and  (these values are given) (these values are given)
 Distribute Distribute 
 Multiply Multiply  and and  to get to get 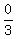 . Now reduce . Now reduce 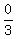 to get to get 
 Add Add  to both sides to isolate y to both sides to isolate y
 Combine like terms Combine like terms  and and  to get to get 
------------------------------------------------------------------------------------------------------------
Answer:
So the equation of the line which goes through the points ( , , ) and ( ) and ( , , ) is: ) is:
The equation is now in  form (which is slope-intercept form) where the slope is form (which is slope-intercept form) where the slope is  and the y-intercept is and the y-intercept is 
Notice if we graph the equation  and plot the points ( and plot the points ( , , ) and ( ) and ( , , ), we get this: (note: if you need help with graphing, check out this solver) ), we get this: (note: if you need help with graphing, check out this solver)
 Graph of Graph of  through the points ( through the points ( , , ) and ( ) and ( , , ) )
Notice how the two points lie on the line. This graphically verifies our answer.
| Solved by pluggable solver: Finding the Equation of a Line Parallel or Perpendicular to a Given Line |
Remember, any two perpendicular lines are negative reciprocals of each other. So if you're given the slope of  , you can find the perpendicular slope by this formula: , you can find the perpendicular slope by this formula:
 where where 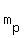 is the perpendicular slope is the perpendicular slope
 So plug in the given slope to find the perpendicular slope So plug in the given slope to find the perpendicular slope
 When you divide fractions, you multiply the first fraction (which is really When you divide fractions, you multiply the first fraction (which is really  ) by the reciprocal of the second ) by the reciprocal of the second
 Multiply the fractions. Multiply the fractions.
So the perpendicular slope is 
So now we know the slope of the unknown line is  (its the negative reciprocal of (its the negative reciprocal of  from the line from the line  ).
Also since the unknown line goes through (-6,4), we can find the equation by plugging in this info into the point-slope formula ).
Also since the unknown line goes through (-6,4), we can find the equation by plugging in this info into the point-slope formula
Point-Slope Formula:
 where m is the slope and ( where m is the slope and ( , , ) is the given point ) is the given point
 Plug in Plug in  , ,  , and , and 
 Distribute Distribute 
 Multiply Multiply
 Add Add  to both sides to isolate y to both sides to isolate y
 Make into equivalent fractions with equal denominators Make into equivalent fractions with equal denominators
 Combine the fractions Combine the fractions
 Reduce any fractions Reduce any fractions
So the equation of the line that is perpendicular to  and goes through ( and goes through ( , , ) is ) is 
So here are the graphs of the equations  and and 
 graph of the given equation graph of the given equation  (red) and graph of the line (red) and graph of the line  (green) that is perpendicular to the given graph and goes through ( (green) that is perpendicular to the given graph and goes through ( , , ) )
|
Go to top
#3
"Write the equation for the line perpendicular to
2x - 5y = 5 and passes through the point (-2, -5).
Enter the variable expression Ax + By separately from the constant term C.
Your response should be given in standard form where A, B and C are the smallest possible integers and A > 0.
First convert 2x - 5y = 5 to slope intercept form
| Solved by pluggable solver: Converting Linear Equations in Standard form to Slope-Intercept Form (and vice versa) |
Convert from standard form (Ax+By = C) to slope-intercept form (y = mx+b)
 Start with the given equation Start with the given equation
 Subtract 2x from both sides Subtract 2x from both sides
 Simplify Simplify
 Divide both sides by -5 to isolate y Divide both sides by -5 to isolate y
 Break up the fraction on the right hand side Break up the fraction on the right hand side
 Reduce and simplify Reduce and simplify
The original equation  (standard form) is equivalent to (standard form) is equivalent to  (slope-intercept form) (slope-intercept form)
The equation  is in the form is in the form  where where  is the slope and is the slope and  is the y intercept. is the y intercept.
|
| Solved by pluggable solver: Finding the Equation of a Line Parallel or Perpendicular to a Given Line |
Remember, any two perpendicular lines are negative reciprocals of each other. So if you're given the slope of  , you can find the perpendicular slope by this formula: , you can find the perpendicular slope by this formula:
 where where 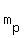 is the perpendicular slope is the perpendicular slope
 So plug in the given slope to find the perpendicular slope So plug in the given slope to find the perpendicular slope
 When you divide fractions, you multiply the first fraction (which is really When you divide fractions, you multiply the first fraction (which is really  ) by the reciprocal of the second ) by the reciprocal of the second
 Multiply the fractions. Multiply the fractions.
So the perpendicular slope is 
So now we know the slope of the unknown line is  (its the negative reciprocal of (its the negative reciprocal of  from the line from the line  ).
Also since the unknown line goes through (-2,-5), we can find the equation by plugging in this info into the point-slope formula ).
Also since the unknown line goes through (-2,-5), we can find the equation by plugging in this info into the point-slope formula
Point-Slope Formula:
 where m is the slope and ( where m is the slope and ( , , ) is the given point ) is the given point
 Plug in Plug in  , ,  , and , and 
 Distribute Distribute 
 Multiply Multiply
 Subtract Subtract  from both sides to isolate y from both sides to isolate y
 Make into equivalent fractions with equal denominators Make into equivalent fractions with equal denominators
 Combine the fractions Combine the fractions
 Reduce any fractions Reduce any fractions
So the equation of the line that is perpendicular to  and goes through ( and goes through ( , , ) is ) is 
So here are the graphs of the equations  and and 
 graph of the given equation graph of the given equation  (red) and graph of the line (red) and graph of the line  (green) that is perpendicular to the given graph and goes through ( (green) that is perpendicular to the given graph and goes through ( , , ) )
|
Now convert 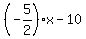 back to standard form back to standard form
If you have any further questions, feel free to ask.
|
|
|
| |