Question 984368: Find the sum of the first n terms of the following series
3X1^2 X5X2^2+7X3^2+---
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I believe what you really need to calculate is


Once you figure out that formula,
 can be proven by induction, like this: can be proven by induction, like this:
1) The formula  is true for is true for  . .
For  , , 
and the formula  , ,
which tells us that
 , ,
which makes the formula true tor  . .
2) We can prove that if  were true for any were true for any  whole number, it would be true for whole number, it would be true for  . .
Term number 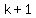 is is
 . .
If  , then , then

=
and that show that the formula is true for  , because the formula says that , because the formula says that

=
=
=
=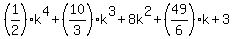
HOW WE CAN GET TO THAT FORMULA:
The sum of terms are of the form 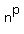 with with  is a polynomial of degree is a polynomial of degree 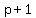 in in  with no independent term. with no independent term.
 , ,
 , and so on. , and so on.
So, the sum of terms of the form  should be should be

Knowing that
 , ,
 , ,
 , and , and
 , ,
we can find  , ,  , ,  , and , and  by solving by solving

|
|
|