Question 984050: A sleeping pill is effective for 75% of the population. If 160 patients are given this sleeping pill then what is the probability or approximate probability that 125 patients or more will sleep better?
I want to determine the binomial probability of exactly x successes in n independent trials, when the probability of exactly one success in one trial is p. Here n = 160 and p=.75
We want to find the success of 125 or more, so that would be patients 125 - 160. My difficulty is writing this "shorthand." I don't want to have to write out 35 equations if I don't have to...
Answer by MathTherapy(10555)   (Show Source): (Show Source):
You can put this solution on YOUR website! A sleeping pill is effective for 75% of the population. If 160 patients are given this sleeping pill then what is the probability or approximate probability that 125 patients or more will sleep better?
I want to determine the binomial probability of exactly x successes in n independent trials, when the probability of exactly one success in one trial is p. Here n = 160 and p=.75
We want to find the success of 125 or more, so that would be patients 125 - 160. My difficulty is writing this "shorthand." I don't want to have to write out 35 equations if I don't have to...
Excel:
BINOMDIST(124,160,.75,1)
This indicates the CUMULATIVE probability of 124, or less, or 0 - 124, which should give you: .79291422
You then subtract this CUMULATIVE probability from 1 to get the CUMULATIVE probability of 125 and more, or 125 - 160
Final result: 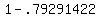 -------> -------> 
You can also do this calc. on the TI-83/84 calculator.
|
|
|