Question 983976: i am the number which will make a rectangle 3 times wide, i am the number which has exactly 8 factors, i am the number which has one of my factor as 4, i am the number which is not a multiple of 5 or 7.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! "I am the number which will make a rectangle 3 times wide" may mean that
if the number is the length of a rectangle,
it will be twice the whole number measurement of the width of that rectangle.
In other words, I take that to mean that the number is a multiple of  . .
That means  is a factor of the mystery number. is a factor of the mystery number.
"I am the number which has one of my factor as 4" means that  is a factor of the mystery number. is a factor of the mystery number.
"I am the number which is not a multiple of 5 or 7" tells us that 5 and 7 are not prime factors of that mystery number, but it is not a particularly useful clue.
Other prime numbers could be factors, like 11, 13, 17, 19, 23, etc .
"I am the number which has exactly 8 factors" is an important clue.
A number  that has that has  and and  , but not , but not  or or  as factors as factors
has a prime factorization of the form
 , with , with  and and  . .
The factors of  , with their prime factorizations, range from , with their prime factorizations, range from
 to to  . .
There are
 different possible exponents for different possible exponents for  , ,
 different possible exponents for different possible exponents for  , ,
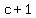 different possible exponents for different possible exponents for  , ,
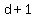 different possible exponents for different possible exponents for  , ,
and so on.
With all the combined possible choices, we can make
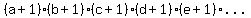 factors. factors.
If  has exactly has exactly  factors, factors,
knowing that  and and  , ,
it is obvious that it must be
 <---> <---> , ,
 <---> <---> , ,
 <---> <---> , ,
 <---> <---> , ,
 <---> <---> , and so on. , and so on.
So,  . .
|
|
|