|
Question 983903: Hi a and b had a total of 27 coins.when a gave 1/4 of his coins to b b had twice as many cojns as
a .b then found out that she had twice as many 20cent coins as 10 cent coins.how much money
did b have in the end.
thank you
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website!  = number of coins a initially had.
 = number of coins b initially had.
You can find and by
solving a system of equations, or by
guess and check.
From there, you can figure out how many coins b has in the end.
Knowing how many coins b has in the end,
and knowing that some of those coins are 10 cent coins,
and the rest are 20 cent coins,
with twice as many 20 cent coins as 10 cent coins,
you can figure out how many coins of each kind b has in the end.
Knowing how many coins of each kind b has in the end, you can figure out how much money those coins amount to.
THE ALGEBRA WAY:
 because initially a and b had a total of 27 coins.
 = number of coins a gave to b.
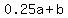 = number of coins a had in the end.
 = number of coins b had in the end.
 because in the end b had twice as many coins as
a.
--> --> --> -->
 ---> ---> ---> ---> ---> --->
So,  = total number of coins b had in the end.
 = total number of coins b had in the end.
 --> ---> --->
 = value of  10-cent coins.
 = value of  20-cent coins.
 = total value of the 10-cent coins and 20-cent coins b had in the end.
THE "GUESS-AND-CHECK" WAY:
Since a and b initially had a total of 27 coins, and a gave 1/4 of his coins to b,
initially a must have had a number of coins that divides by 4 evenly, and is less than 27,
such as 4, or 8, or 12, or 16, or 20, or 24.
If it was 4, b would have initially had 27-4=23 coins;
a would have given b just 1 coin, keeping the other 4-1=3 coins,
and b would have had 23+3=26 coins in the end.
Those 26 coins are a much greater number of coins than twice the 3 coins a had in the end.
So, b must have started with less than 23 coins and a must have started with more than 4 coins.
If a started with 8 coins, a would have given 2 of them to b, ending with 8-2=6 coins,
while b would have started with 27-8=19 coins, and would have ended with 19+2=21.
Those 21 coins are a greater number of coins than twice the 6 coins a had in the end.
So, a must have started with more than 8 coins.
If a started with 12 coins, a would have given 3 of them to b, ending with 12-3=9 coins,
while b would have started with 27-12=15 coins, and would have ended with 15+3=18,
which is twice as many coins as the 9 coins a ended up with.
So, a started with 12 coins, and b had 18 coins in the end.
Those 21 coins are a greater number of coins than twice the 6 coins a had in the end.
From there you can continue as above, or guess-and-check to find how many of those 18 coins are 10 cent coins.
If at the end just 1 of the coins b had was a 10-cent coin, b would have had 2 20-cent coins for a total of 1+2=3 coins.
So the number of 10-cent coins must b had in the end must have been more than 1.
If at the end just 5 of the coins b had were 10-cent coins, b would have had twice 5, or 10 20-cent coins for a total of 5+10=15 coins.
Since b had 18 coins at the end, and 18 is more than 15,
the number of 10-cent coins must b had in the end must have been more than 5.
If at the end 6 of the coins b had were 10-cent coins, b would have had twice 6, or 12 20-cent coins for a total of 6+12=18 coins.
Since b had 18 coins at the end, that is the mix of coins b had at the end,
and 6 10-cent coins plus 12 20-cent coins make $3.00.
|
|
|
| |
