Question 983779: Please help me with the equation below:
Identify the intercepts, asymptotes, and "holes" on this rational equation:
f(x) = x^3+4x^2-5x/x^2-1
Found 2 solutions by solver91311, KMST:
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website!
1. Find the  -intercept. Substitute zero for -intercept. Substitute zero for  . If the function is defined at . If the function is defined at  , then the value of the function at , then the value of the function at  is the is the  -coordinate of the -coordinate of the  -intercept. Remember that a -intercept. Remember that a  -intercept has the form -intercept has the form )
2. Find the  -intercept(s). Set the numerator of the rational function equal to zero and solve for all real number roots. Each real number root of the numerator will be an -intercept(s). Set the numerator of the rational function equal to zero and solve for all real number roots. Each real number root of the numerator will be an  -coordinate of an -coordinate of an  -intercept. Remember that an -intercept. Remember that an  -intercept has the form -intercept has the form )
3. Find any vertical asymptotes or holes. Factor both the numerator and denominator polynomials completely. If there is a factor that is in both the numerator and denominator, the value of  when that factor is set equal to zero is the location of a "hole". If there is a factor in the denominator that is not in the numerator, the value of when that factor is set equal to zero is the location of a "hole". If there is a factor in the denominator that is not in the numerator, the value of  when that factor is set equal to zero is the location of a vertical asymptote. when that factor is set equal to zero is the location of a vertical asymptote.
4. Find any horizontal or oblique asymptotes.
If the degree of the numerator is smaller than the degree of the denominator, there is a horizontal asymptote at 
If the degree of the numerator is equal to the degree of the denominator, then there is a horizontal asymptote at  where where  is the lead coefficient of the numerator polynomial and is the lead coefficient of the numerator polynomial and  is the coefficient of the denominator polynomial. is the coefficient of the denominator polynomial.
If the degree of the numerator is one greater than the degree of the denominator then there is an oblique asymptote. Using Polynomial Long Division, find the quotient of the numerator divided by the denominator, excluding any remainder. This quotient is the oblique asymptote function descriptor.
If you are unsure of the process for Polynomial Long Division, see: Purple Math Polynomial Long Division
John

My calculator said it, I believe it, that settles it

Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I assume you mean  . .
The y-intercept is the point where the graph crosses the y-axis,
and for all points on the y-axis  , ,
so the y-intercept is  . .
The function crosses the y-axis at the point with  , ,
The  is the point (0,0), the origin. is the point (0,0), the origin.
Factoring numerator and denominator, we get
 . .
For  , the function is not defined, because the denominator is zero. , the function is not defined, because the denominator is zero.
However for values of  around around   has a value. has a value.
There is just a  at at  . .
Otherwise, for  , the expression simplifies to , the expression simplifies to
 , ,
When a factor in the 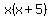 numerator is zero, numerator is zero,  , ,
and the graph crosses the x-axis, with 
The points where that happens are the  : :
 , and , and
 ---> ---> . .
So the graph crosses the x-axis at (0,0) (we knew that point) and at (-5,0).
Also, for  , we see that , we see that  is undefined for is undefined for  , because the denominator is zero. , because the denominator is zero.
For values of  very close to very close to  , ,
the numerator, the quadratic polynomial  , and , and
as  approaches approaches  , ,  approaches approaches  . .
On the other hand, as  approaches approaches  , ,
the denominator,  , approaches zero. , approaches zero.
As a consequence, the absolute value of the quotient  grows without bounds. grows without bounds.
That makes  a a   . .
Also, for  . .
and  approaches zero as approaches zero as 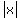 increases. increases.
That makes  an an  . .
With all that information, we can sketch the graph of  , ,
which looks like this 
NOTE:
 should be written as f(x)=(x^3+4x^2-5x)/(x^2-1), should be written as f(x)=(x^3+4x^2-5x)/(x^2-1),
because according with the algebra conventions known as "order of operations" rules,
multiplication and divisions are done before addition and subtraction, so
x^3+4x^2-5x/x^2-1 = 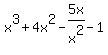 . .
The long horizontal line separating  from from  is a very efficient grouping symbol: is a very efficient grouping symbol:
it saves you from writing two pairs of parentheses.
However, when you have to key in symbols one at a time,
you have to key in all those parentheses that are implied.
Otherwise, you can get in trouble.
 (rounded to 3 decimal places). (rounded to 3 decimal places).
Most calculators know about order of operations,
and if you key in
0.735 - 0.004 / 0.720 - 0.008 =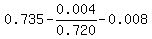 , ,
you will get  (rounded to 3 decimal places). (rounded to 3 decimal places).
|
|
|