Question 983734: Please solve the equation for the interval [ 0, 2pi ]:

Thank you!
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website!
One solution is
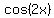 = =  . .
It gives  = =  , where , where  is an arbitrary integer (k = 0, +/-1, +/-2, . . . ). is an arbitrary integer (k = 0, +/-1, +/-2, . . . ).
Hence  = = 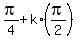 . .
It gives for k = 0, 1, 2, 3
 = =  , , 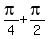 = =  , , 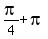 = =  , , 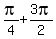 = =  . .
Next, if 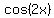 is not zero, then you can reduce the original equation to the form is not zero, then you can reduce the original equation to the form
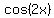 = =  . .
dividing it by 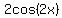 . .
It gives you
 = +/- = +/- + +  , where , where  is an arbitrary integer (k = 0, +/-1, +/-2, . . . ). is an arbitrary integer (k = 0, +/-1, +/-2, . . . ).
Hence  = +/- = +/- + +  . .
It gives for k = 0, 1, 2, 3,
 = =  , , 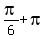 = =  , , 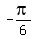 , , 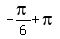 = = 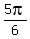 . .
Answer.  = =  , ,  , ,  , ,  . .
 = =  , ,  , , 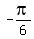 , , 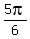 . .
|
|
|