Question 983211: Ann goes swimming regularly she wants to improve her fitness, so she
decides to swim 10 lengths in the first session and increase the number of
lengths she swims by 2 every session. When she reaches 50 lengths in a
session, she will not increase the number any further. If Ann asks her
friend Joy to come swimming with her, Joy starts coming at Sue's 8th
session, Joy starts to swim 15 lengths and increases the number of
lengths by 5 each time. After how many of Joy's sessions does she swim
the same number of lengths as Ann?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE FIFTH GRADER WAY:
Let me make a table.

On Joy's 4th sessions, after  sessions, sessions,
she swims the same number of lengths as Ann.
USING ALGEBRA BEFORE LEARNING ABOUT SEQUENCES:
Ann is  sessions "ahead" of Joy, sessions "ahead" of Joy,
so when it is after  sessions for Joy, sessions for Joy,
it is after 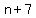 sessions for Ann. sessions for Ann.
After  sessions, it is session sessions, it is session  for Joy, for Joy,
and she swims  lengths. lengths.
At that time, Ann is on session  , ,
had previously completed 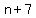 sessions, sessions,
and swims  lengths. lengths.
When Joy swims the same number of lengths as Ann,
 --> --> --> --> --> --> --> --> --> -->
USING SEQUENCES:
The number of lengths swam by Ann forms an arithmetic sequence/progression
with first term  and common difference and common difference  , ,
so the number of lengths she swims in session number  is is
 . .
The number of lengths swam by Joy forms an arithmetic sequence/progression
with first term  and common difference and common difference  , ,
so the number of lengths she swims in session number  is is
 . .
After  sessions, Joy is in session number sessions, Joy is in session number  , ,
and swims  lengths. lengths.
At the same time, Ann, who swam  sessions without Joy, sessions without Joy,
is in her session number  , and swims , and swims
 lengths. lengths.
If Ann and Joy swin the same number of lengths,
 --> --> --> --> --> --> --> --> --> -->
|
|
|