SOLUTION: Hi, Prof has given us this for a bit of homework can any one help me out? you can ignore the brackets around the fractions only way I could format it given {{{ f(x,y) = (

 

Take partial derivatives with respect to x and y.





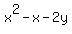
Set them = 0, 



Solve that 
Get (x,y) = (0,0), (5,10) 




Critical points (x,y,z) = (0,0,1), (5,10,-65/6)

Second partial test.  Get the four second partial derivatives:

 
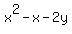
 at (0,0) is -1, at (5,10) is 9
   at (0,0) is -2, at (5,10) is -2


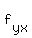
   at (0,0) is -2, at (5,10) is -2  
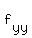
    at (0,0) is 1,  at (5,10) is 1



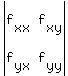We test (x,y) = (0,0)



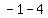
So the point (0,0,10) is a saddle point.

We test (x,y) = (5,10)



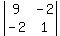
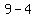
So the point (5,10,65/6) is determined by the sign of fxx,
which is 9, which is positive, so concave upward there and is a
relative minimum. 

Edwin