Question 982534: I need help with this problem? The equation of a hyperbola is  Write the equation of the hyperbola in standard form and find the coordinates of the center, the coordinates of the vertices, and the equation of the asymptotes. Then graph the hyperbola. Write the equation of the hyperbola in standard form and find the coordinates of the center, the coordinates of the vertices, and the equation of the asymptotes. Then graph the hyperbola.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
 ....complete square ....complete square








The standard form of an hyperbola with the transverse axis being vertical.

The center of the hyperbola is at the point (  , , ) or ( ) or ( , , ) )
 and and  , so , so
semimajor axis length 
semiminor axis length 
The foci are  units from the center of the hyperbola and is calculated from units from the center of the hyperbola and is calculated from  . .
 => => => =>
The foci are therefore, (  , , 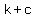 ) or ( ) or (  , ,  ) )
or ( , ,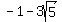 ) and ( ) and ( , ( , (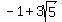 ) )
=>( , ,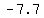 ) and ( ) and ( , , 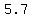 ) )
The vertices are a units from the center of the hyperbola, (  , , 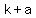 ) and ( ) and (  , , 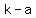 ) )
or (  , ,  ) and ( ) and (  , ,  ) )
asymptotes:



|
|
|