Question 982458: sir, maam
good day pls help me with my homework pls i need to answer this in 3 hour because i am confused so that i cannot do it on my house pls help me
1.Two altitudes of an isosceles triangle areequal to 20 cm and 30 cm. Determine the baseangles of the triangle\
2.Two altitudes of an isosceles triangle areequal to 20 cm and 30 cm. Determine the baseangles of the triangle
Found 2 solutions by KMST, ikleyn:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The area of a triangle is 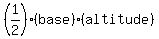 . .
The sides of an isosceles triangle come in two lengths:
the length of the two congruent legs, and
the length of the other side, which we usually consider the base.
However, you can take any side of a triangle as the base,
and the perpendicular to that base from the other vertex is the altitude,
so, in that case,
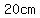 is the altitude to a base measuring is the altitude to a base measuring   , and , and
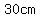 is the altitude to a base measuring is the altitude to a base measuring   . .
Calculating the area both ways, we get the same result, so
 ---> ---> ---> ---> . .
Could the legs of the isosceles triangle measure   ? ?
If so, the triangle looks like this
 and and  ---> --->  (rounded). (rounded).
Could the legs of the isosceles triangle measure   ? ?
 We would have an angle We would have an angle  such that such that
 ---> ---> (rounded). (rounded).
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website!
1. First, let us assume that the altitude of 20 cm long goes to the base  and the altitude of 30 cm long goes to the lateral side and the altitude of 30 cm long goes to the lateral side  . .
Then you have these expressions for the area of the triangle:
 = =  . .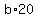 = =  . .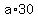 . .
It implies that 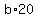 = = 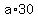 . .
Hence,  = = 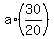 = = 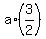 . .
Now consider the right-angled triangle formed by the base, by the altitude of 20 cm long and by the lateral side  . .
This right-angled triangle has the hypotenuse of the length  and the leg of the length and the leg of the length  (yes, it is half of the base of the triangle, (yes, it is half of the base of the triangle,  = = 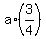 ). ).
I believe (I hope) you just made a sketch of your triangle. It will help you to see what I am saying.
Therefore,  = = 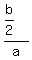 = = 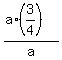 = =  , where , where  is the angle at the base of our isosceles triangle. is the angle at the base of our isosceles triangle.
Thus, in this case  = =  and and  = = 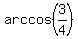 . .
2. Next, let us consider the other configuration when the altitude of 30 cm long goes to the base  and the altitude of 20 cm long goes to the lateral side and the altitude of 20 cm long goes to the lateral side  . .
Then you have these expressions for the area of the triangle:
 = =  . .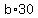 = =  . .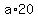 . .
It implies that 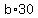 = = 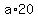 . .
Hence,  = = 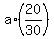 = = 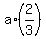 . .
Now consider the right-angled triangle formed by the base, by the altitude of 30 cm long and by the lateral side  . .
This right-angled triangle has the hypotenuse of the length  and the leg of the length and the leg of the length  (which is half of the base of the triangle, (which is half of the base of the triangle,  = = 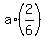 ) = ) = 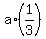 . .
Again, I hope you just made a sketch of your triangle.
Therefore,  = = 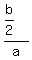 = =  = =  . .
Thus, in this case  = =  and and  = =  . .
Answer.  = =  or or  = = 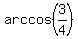 . .
|
|
|