SOLUTION: Find all polar coordinates of point P where P = (7, pi/3)? Can someone please walk me through this problem?

Below is your polar point 

 

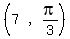plotted. It is on the circle with radius r=7, and which makes an angle of  
with the right side of the x-axis.



Now it is quite obvious that we can add any multiple of 2p 
to that and get the same point in the first quadrant.  So the
point could also have coordinates:

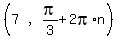, when n is any integer

However what is not so obvious is that we can get to the same point
not only from the 1st quadrant, but also from the opposite quadrant,
which is the 3rd quadrant.

We can think of starting at the 3rd quadrant angle which has  
as its referent angle, which is , and taking r as a 
negative number instead of a positive number, and from the 3rd quadrant 
think of going "back up through" the origin (or pole) to the 
point's position up in the 1st quadrant, which is considered as going
-7 units in the direction of  in the 3rd quadrant. We can 
also obviously add any multiple of 2p to .  

Therefore the same point can also have the polar coordinates

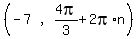, where n is any integer 
   
There are infinitely many sets of POLAR coordinates for a point, but
only one set of RECTANGULAR coordinates (x,y).

Edwin