SOLUTION: What is the sum of the infinite geometric series 3/4-9/16+27/64-81/256+ ..? A. 3 b. 1 C.3/4 D. 3/7

Instead of doing your problem for you, I will do one EXACTLY IN EVERY
DETAIL like yours, so that when you do yours, you can use this as a
model.

I will find the sum of this infinite geometric series instead:



We should first check to see if it really is a geometric series, for sometimes
books contain errors/typos.  If it is a geometric series then this must be true:



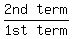
So we calculate the three ratio to see if they are all equal:







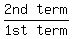
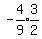
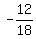
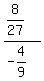
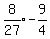
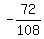
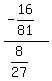
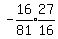
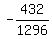
They are all the same so it is a geometric series with common ratio = 

It is a geometric series with a defined sum when taken to infinitely many
terms because the ratio  is greater than -1 and less than +1.

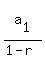, where a1 = 1st term = 



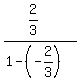
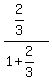
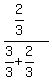
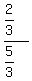
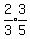
Answer to this problem = 

Now do your problem EXACTLY the same way.

Edwin