Question 982206: Arithmetic Sequence Problem:
A mosaic in the shape of an equilateral triangle is 25 ft on each side. Each tile in the mosaic is in the shape of an equilateral triangle, 12 inches to a side. The tiles are alternate in colour like △▾△ (sorry I cant show the picture) . How many tiles of each colour will be needed?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Each tile in the mosaic is in the shape of an equilateral triangle,
 to a side. to a side.
On the base of that triangular mosaic,
you have the bases of  tiles of color tiles of color  . .
Tiles of color  will be at all 3 vertices of the triangular mosaic, will be at all 3 vertices of the triangular mosaic,
and all 3 sides of the triangular mosaic would look just the same,
so it does not matter which one I choose to call the base of the triangular mosaic.
In between the  base-down, vertex-up triangles of color base-down, vertex-up triangles of color  , ,
there will be  base-up, vertex-down triangles of color base-up, vertex-down triangles of color  , ,
completing the first row/layer of tiles at the base of the triangular mosaic.
Atop each of those  base-up, vertex-down triangles of color base-up, vertex-down triangles of color  , ,
there will be one base-down, vertex-up triangle of color  , ,
for a total of  base-down, vertex-up triangles of color base-down, vertex-up triangles of color 
on the second row of the triangular mosaic.
In between the  base-down, vertex-up triangles of color base-down, vertex-up triangles of color  on the second row, on the second row,
there will be  base-up, vertex-down triangles of color base-up, vertex-down triangles of color  , ,
completing the second row/layer of tiles at the base of the triangular mosaic.
That patter repeats, so you have
 tiles of color tiles of color  , and , and
 . .
Those numbers are the sums of the  and and  first terms of the arithmetic sequence with first term first terms of the arithmetic sequence with first term  and common difference and common difference  . .
The easiest way to calculate the sum 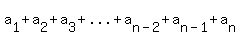 when you know when you know
the number  of terms you are adding, of terms you are adding,
the first term  you are adding, and you are adding, and
the last term  you are adding is you are adding is
 . .
So,

and

|
|
|