SOLUTION: Please could you help explain how to answer this question. I can understand part i but not part ii. i) On an Argand diagram show the region R for which |z-5+4i| ≤ 3 For

Algebra ->  Complex Numbers Imaginary Numbers Solvers and Lesson -> SOLUTION: Please could you help explain how to answer this question. I can understand part i but not part ii. i) On an Argand diagram show the region R for which |z-5+4i| ≤ 3 For       Log On


   

Question 981555: Please could you help explain how to answer this question.
I can understand part i but not part ii.
i) On an Argand diagram show the region R for which |z-5+4i| ≤ 3
For this part |z-(5-4i)| ≤ 3 and the point is 5-4i on an argand diagram and z has a radius of 3 which is a shaded in circle. Textbook answer shows this is correct.
ii) Find the greatest and least values of |z+3-2i| in the region R.
This is the part I don't understand.
I tried|z-(-3+2i)|and then trying to find the modulus which is the square root of 13.
The answer given in the book is 7,13 although I can't figure out how to get there.
Any help given would be fantastic.




Answer by Edwin McCravy(20059) About Me  (Show Source):
You can put this solution on YOUR website!



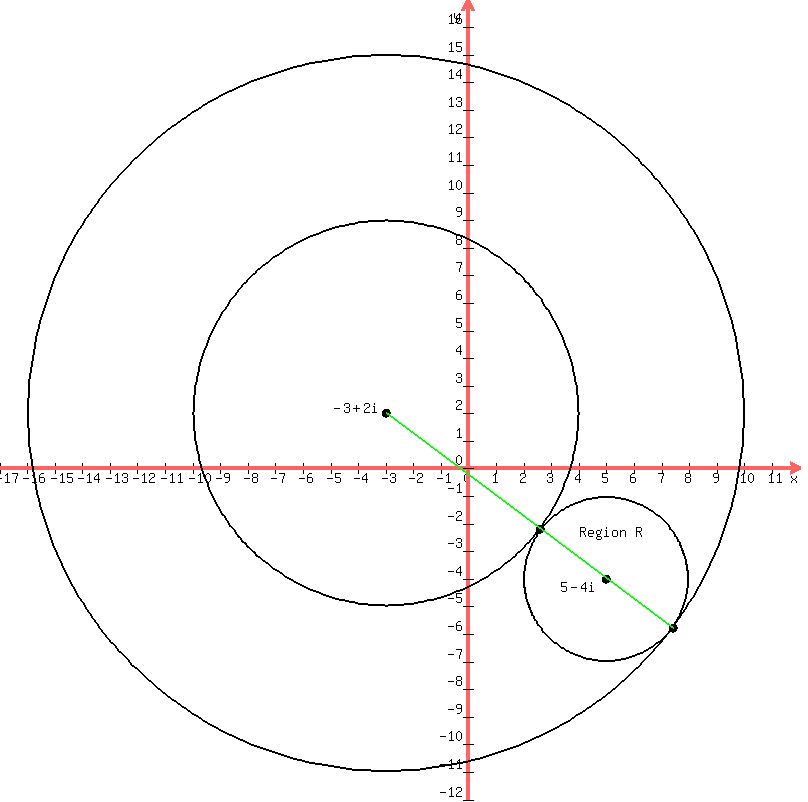
We draw two circles |z+3-2i|=r, one with the shortest possible
radius r that puts the circle in the region R, and the other
with the longest possible radius which puts the circle in
the region R.  They will be tangent to the disk with is Region
R.  Then all we have to do is calculate those two radii.  If 
your book answers are correct those two radii should be 7 and 13.

So just find the distance between the centers of the two
circles, -3+2i and 5-3i, which will be 10, then subtract the
radius 3 to get the minimum 7 and add it to get the maximum 13.

If you have any questions, ask them in the thank-you note
form below.

Edwin